Maths ...

Problème n ° 98

concours de beauté chez les grenouilles ! le corrigé

• Enoncé du problème n°98

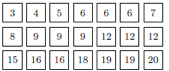
  Lors d’un concours de beauté, des grenouilles sont notées de 0 à 20 par un jury de crapauds. Voici les notes obtenues par les 21 candidates :

  

  Pour la renommée du concours, le président du jury décide d’augmenter la moyenne de 1 point.

  Par souci de discrétion, il doit changer le moins de notes possibles et ne doit modifier ni la médiane, ni l’étendue.

  Conseiller le président du jury pour le choix de ces nouvelles notes.

• Correction du problème n°98

  • Il y a 21 candidates.
  • La moyenne est égale à 10.
  • L’étendue est égale à 17.
  • La médiane est égale à la onzième valeur ordonnée, c’est-à-dire 9.

  Pour obtenir une moyenne égale à 11, le jury doit attribuer 21 points supplémentaires.
  Essayons de modifier seulement deux notes. On voit très vite que l’on doit attribuer au moins 11 points à une note inférieure ou égale à la médiane, et la médiane se trouve donc changée. On ne peut donc pas ajouter 21 points en changeant uniquement deux notes.
  En modifiant trois notes, plusieurs solutions sont possibles.
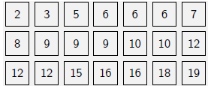
  Voici une solution, basée sur l’égalité 21 = 6 + 6 + 9.

  • On supprime un 3 et on remplace par un 9 ;
  • on supprime un 10 et on remplace par un 16 ;
  • on supprime un 10 et on remplace par un 19.

    

    Voici une autre solution, basée sur l’égalité 21 = 2 + 9 + 10.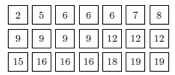
    • On supprime un 2 et on remplace par un 4 ;
    • on supprime un 10 et on remplace par un 19 ;
    • on supprime un 10 et on remplace par un 20.

    

    Les caractéristiques statistiques données plus haut sont gardées.

Yannick BARRAL

Maths ...

Problème n ° 98

concours de beauté chez les grenouilles !

Yannick BARRAL

Maths ...

Problème n ° 97

Histoire de fourmis, le corrigé

• Enoncé du problème n° 97

  Des fourmis se déplacent, en ligne droite, à la queue leu leu, à vitesse constante, en formant une colonne de 50 cm de long. La dernière fourmi du groupe décide d’aller ravitailler la fourmi chef, et pour cela elle rejoint la tête de la colonne puis, sa mission étant accomplie, retourne aussitôt à la queue de la colonne.
  Sachant que, pendant cet aller-retour, la vitesse de cette fourmi est restée constante et que la colonne a parcouru 50 cm, quelle est la distance parcourue par la fourmi ravitailleuse ?

• Correction du problème n°97

  Soit $v$ la vitesse de la colonie de fourmis en centimètres par seconde,
  $V$ la vitesse de la fourmi,
  $t_1$ le temps aller de la fourmi en secondes
  et $t_2$ le temps de retour.
  La distance aller est $d_1=Vt_1=vt_1+50$.
  La distance retour est $d_2=Vt_2=50-vt_2$.
  On en déduit $t_1=\dfrac{50}{V-v}$ et $t_2=\dfrac{50}{V+v}$.
  On a donc $$50= \dfrac{50}{V-v}+\dfrac{50}{V+v}$$ En posant $X=\dfrac{V}{v}$, on a : $X^2-2X-1=0$
  Cette équation a deux solutions : $X=1\pm\sqrt 2$ . On ne retient que $X=1+\sqrt 2$ car $1-\sqrt 2<0$ et $ \dfrac{V}{v}> 0$.
  On déduit donc $X=(1+\sqrt2) $, ce qui donne $V=(1+\sqrt 2) v$.
  La distance parcourue est $50(1+\sqrt 2)$ cm.

Yannick BARRAL