Problème n°10 : Histoire de boulets ...
Enoncé du Problème n ° 32
Un problème classique, autrefois dans les écoles militaires, constituait à déterminer le nombre de boulets que l'on entassait à proximité des canons.Les entassements pratiqués étaient sous forme de pyramide à base carrée ou à base triangulaire.
- Déterminer en fonction de $k$ le nombre de boulets d'une couche.
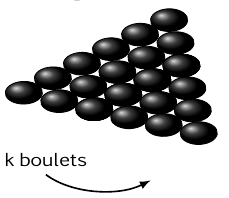
- Montrer que le nombre de boulets à $n$ couches est $\dfrac{n(n+1)(n+2)}{6}$.
- Montrer qu'avec les boulets d'une pyramide à 8 couches et ceux d'une pyramide à 14 couches il est possible de constituer une autre pyramide. ( préciser le nombre de couches) .
Auteur : Luc GIRAUD