Problème n°17 : La fourmi et le miel
Enoncé du Problème n ° 17
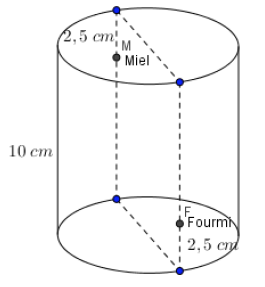
- On place une goutte de miel à l’intérieur d’un verre cylindrique, à 2,5 cm du bord.
- Une fourmi se trouve aussi sur le verre, en face de la goutte de miel, mais sur la paroi extérieure, à 2,5 cm du fond.
- La hauteur du verre est de 10 cm et la circonférence de base est de 25 cm.
- Quel chemin doit suivre la fourmi sur les parois du verre pour atteindre le miel en parcourant le minimum de distance possible ? Quelle est cette distance minimale ?
Indication : on pourra faire un patron de la surface latérale du cylindre sur lequel on placera la fourmi et la goutte de miel.
Auteur : Lionel DARIE