Problème n° 14: un empilement; le corrigé

• On réalise un empilement avec quatre oranges, assimilées à des sphères de rayon 4 cm ; chacune est en contact avec les trois autres.
• Calculer la hauteur $h$ de cet empilement.

Indication : utiliser le résultat suivant : « Dans un tétraèdre régulier $ABCD$, le projeté orthogonal d’un sommet, $A$ par exemple, sur la face opposée $(BCD$) est le centre du triangle équilatéral $BCD$ ».

 

 

Auteur : Lionel DARIE

Auteur : Lionel DARIE

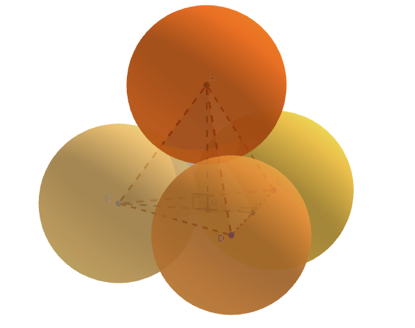
• On appelle $B, C$ et $D$ les centres respectifs des trois oranges posées sur le plan de la table et $A$ le centre de l’orange au sommet, posée sur les trois autres. $ABCD$ est alors un tétraèdre régulier, de côté $a = 2R$, où $R$ est le rayon d’une orange. Ici, $R = 4$ cm donc $a = 8$ cm.
• Montrons d’abord que la hauteur d’un tétraèdre régulier de côté $a$ est $d = a \sqrt{\dfrac{2}{3}}$:
• Soit $G$ le projeté orthogonal de $A$ sur la face opposée $(BCD)$. $G$ est le centre du triangle équilatéral $BCD$. $G$ est à la fois le centre de gravité, le centre du cercle circonscrit, le centre du cercle inscrit etc.

• Dans le triangle équilatéral $BCD$, on note $H$ le milieu de $[CD]$. $[BH]$ est une médiane de $BCD$, donc passe par $G$. On sait que le centre de gravité d’un triangle est situé au deux tiers de la médiane, en partant du sommet donc : $$BG = \dfrac{2}{3}BH$$

• Or, $BCH$ est un triangle rectangle en $H$ car dans un triangle équilatéral, les médianes sont aussi des hauteurs. D’après le théorème de Pythagore : $$BC^2 = CH^2 + BH^2$$ donc $BH^2 = BC^2– CH^2$
  donc $BH^2= a^2 – \left( \dfrac{1}{2} a\right) ^2 = \dfrac{3}{4} a^2$
  donc $BH = a\dfrac{\sqrt{3}}{2} $ . Ainsi, $BG = = \dfrac{2}{3}BH= \dfrac{2}{3}\times a\dfrac{\sqrt{3}}{2} $
  donc $$BG = \dfrac{\sqrt{3}}{3}a$$
• La triangle $ABG$ étant rectangle en $G$, on peut à nouveau appliquer le théorème de Pythagore :
  $AB^2= AG^2 + BG^2$
  donc $AG^2 = AB^2 – BG^2$ donc $AG^2 = a^2– \dfrac{1}{3} a ^2= \dfrac{2}{3}a^2$ d’où $AG = a\sqrt{\dfrac{2}{3}}$
• Finalement, la hauteur totale de notre empilement d’oranges est :
  $h = R + d + R $ soit : $ h = 2R + a\sqrt{\dfrac{2}{3}} $ et comme $a = 2R$, $$h = 2R \left( 1 + \sqrt{\dfrac{2}{3}} \right).$$ Avec $R = 4 $cm, on obtient $h = 8 \left( 1 + \sqrt{\dfrac{2}{3}} \right)$ soit $ h \approx 14,53$ cm.