Maths ...

Problème n ° 119

Papous pas papas à poux, le corrigé

• Enoncé du problème n° 119

  En Papouasie, il y a des Papous et des pas Papous.
  Parmi les Papous, il y a des Papous papas et des Papous pas papas.
  Mais il y a aussi des papas pas Papous et des pas Papous pas Papas.
  De plus, il y a des Papous pas papas à poux et des papas pas Papous à poux.
  Mais il n’y a pas de papas Papous à poux ni de pas Papous pas papas à poux. Combien y a-t-il de types de Papous en Papouasie ?

• Correction du problème n°119

  On peut utiliser un arbre de choix pour représenter la situation :
  
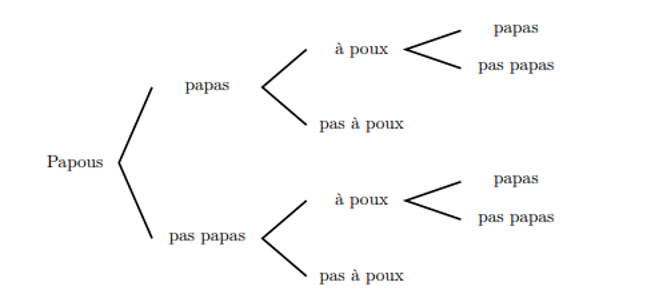
  On obtient ainsi :

  • des Papous papas à poux papas ;
  • des Papous papas à poux pas papas ;
  • des Papous papas pas à poux ;
  • des Papous pas papas à poux papas ;
  • des Papous pas papas à poux pas papas ;
  • des Papous pas papas pas à poux.

  C’est-à-dire six types de Papous.

Yannick BARRAL

Maths ...

Problème n ° 119

Papous pas papas à poux

Yannick BARRAL

Maths ...

Problème n ° 118

Un troupeau en extinction, le corrigé

• Enoncé du problème n° 118

  Un éleveur de Math-City conduit des vaches le long du fleuve.
  Chaque vache lui coûte 15 € de nourriture par jour, et lui-même a des dépenses personnelles quotidiennes de 30 €.
  Chaque soir, il dépose une vache dans la localité où il passe ; son troupeau diminue donc d’une unité.
  Après avoir déposé sa dernière vache, il fait son bilan et se dit : « Tiens, le nombre d’euros que j’ai dépensés est le plus petit nombre qui est divisible par 1, par 2, par 3, par 4, par 5, par 6, par 7, par 8, par 9 et par 10. »
  Combien le troupeau comportait-il de vaches au départ ?

• Correction du problème n°118

  Le plus petit nombre qui est divisible par 1, par 2, par 3, par 4, par 5, par 6, par 7, par 8, par 9 et par 10 est : $$2 \times 3 \times 4 \times 5 \times 7 \times 3 = 2 520 $$ C’est donc la somme dépensée par l’éleveur.
  Le dernier jour, il a dépensé 15 € pour sa vache et 30 € pour lui, soit au total $15 + 30$.
  L’avant-dernier jour, il avait encore deux vaches.
  Sa dépense était égale à $2 \times 15 + 30$.
  Et le jour précédent,$ 3 \times 15 + 30$. Et ainsi de suite.
  Si $n$ désigne le nombre de vaches au départ, et donc le nombre de jours qu’a duré le voyage, la dépense totale (2 520€) est : $$(1 + 2 + 3 + \cdots+ n)\times 15 + 30 n $$ On a donc : $$\dfrac{n(n + 1)}{2}\times 15 + 30 n = 2 520$$ Ce qui se simplifie en : $$n^2 + 5 n - 336 = 0 $$ D’où $n = 16$. Le troupeau comprenait 16 vaches au départ.

Yannick BARRAL