Maths ...

Problème n ° 117

Le verre penché, le corrigé

• Enoncé du problème n° 117

  Un verre hémisphérique est rempli sur la moitié de sa hauteur.
  
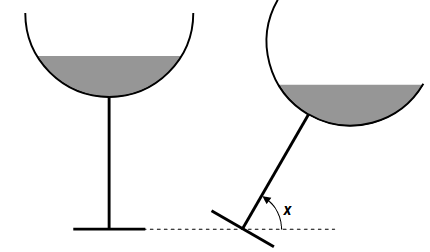
  Quel est l'angle minimum x selon lequel on peut pencher ce verre sans renverser de liquide ?

• Correction du problème n°117

  
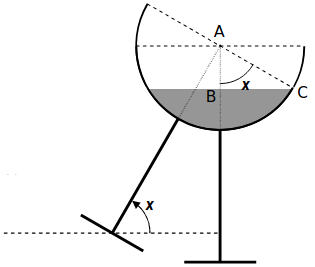
  D'après les données de la figure le triangle $ABC$ est rectangle en $B$ et $AB=\frac{AC}{2}$.
  On a alors : $$\cos x=\frac{AB}{AC}=\frac{1}{2}$$ Soit : $$x=60^{\small\circ}$$
  Autrement dit, on peut pencher le verre de $30^{\small\circ}$ par rapport à la verticale.

Simon Marseille

Maths ...

Problème n ° 117

Le verre penché

Simon Marseille

Maths ...

Problème n ° 116

Lutter pour survivre, le corrigé

• Enoncé du problème n° 116

  Sur une île chaque jour et dans cet ordre, chaque loup tue un mouton, chaque mouton tue un serpent et chaque serpent tue un loup. Après 10 jours il ne reste plus sur l'île qu'un mouton et aucun autre animal.
  Combien y avait-il d'animaux de chaque espèce au départ ?

• Correction du problème n°116

  Soient $L_n$, $M_n$ et $S_n$ le nombre respectif de loups, moutons et serpents après $n$ jours.
  On a alors :

  • $M_n=M_{n-1}-L_{n-1}$
  • $S_n=S_{n-1}-M_n$
  • $L_n=L_{n-1}-S_n$

  On obtient alors :

  • $S_n+M_n=S_{n-1}$
  • $L_n+S_n=L_{n-1}$
  • $M_n+L_{n-1}=M_{n-1}$ soit $M_{n-1}=M_n+L_n+S_n$

  On sait que $M_{10}=1$, $S_{10}=0$ et $L_{10}=0$.
  Avec un tableur, on obtient :
  

Simon Marseille