Enoncé de l'énigme n° 2 (Lycée 1)

Correction de l'énigme n° 2 (Lycée 1)

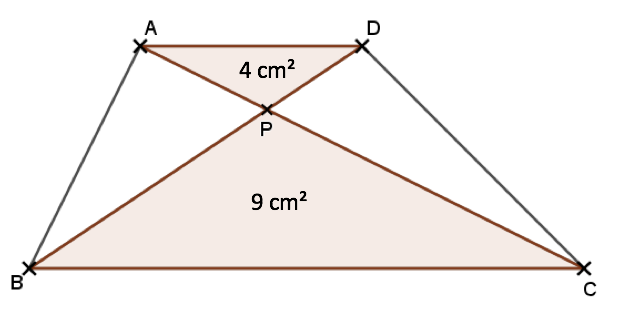
• On sait que (AD) et (BC) sont sécantes en P et que (AD) // (BC). On a donc, d'après le théorème de Thalès : $$\dfrac{PA}{PC} = \dfrac{PD}{PB}=\dfrac{AD}{CB}$$
• Notons $k$ la valeur de ce quotient.
  On a $PA=k\times PC$ , $PD=k\times PB $ et $AD=k\times CB $
  donc le triangle $APD$ est une réduction de coefficient $k$ du triangle $BPC$ ( ce ne peut pas être un agrandissement car l'aire du triangle $APD$ est inférieure à celle du triangle $BPC $).
  L'aire du triangle $APD$ est donc égale au produit de l'aire du triangle BPC par $k^2$.
  Comme l'aire du triangle $APD$ est égale à 4 cm$^2$, et comme celle du triangle $BPC$ est égale à 9 cm $^2$, on a : $$k^2= \dfrac{4}{9}$$ donc comme $k>0$, on déduit $k= \dfrac{2}{3}$

Auteur : Delphine GUILLERMARD

Enoncé de l'énigme n° 1 (Lycée 1)

Correction de l'énigme n° 1 (Lycée 1)

Soit $x$ le nombre de billets de 5 € et $y$ le nombre de billets de 10 €. La somme d’argent, en €, dont dispose Sophie est donc : $S= 5 x+ 10 y$. De plus, on a :$x +y = 20$.

Si maintenant désigne le nombre de billets de 10 € et le nombre de billets de 5 € alors la somme d’argent, en €, dont disposerait Sophie serait : $S’= 10x + 5y =S + 70$.

Soit $10x + 5y = 5x + 10 y+ 70$. Soit $5x − 5y = 70$.

Soit, en simplifiant par 5, on obtient : $x− y= 14$.

Il faut donc résoudre le système : $$\left\lbrace \begin{array}{ll} x + y &= 20~\\ x-y &= 14 \end{array} \right. \iff \left\lbrace \begin{array}{l } y = 20-x~\\ x+x-20 = 14 \end{array} \right. \iff \left\lbrace \begin{array}{l } y = 20-x~\\ 2x-20 = 14 \end{array} \right. \iff \left\lbrace \begin{array}{l } y = 20-x~\\ 2x = 34 \end{array} \right. \iff \left\lbrace \begin{array}{l } y = 20-17=3~\\ x = 17 \end{array} \right. $$ La solution de ce système est le couple (17 ; 3).


Sophie possède 17 billets de 5 € et 3 billets de 10 €.

Elle possède alors $S= 5\times 17 10\times 3 = 115$ €.

Auteur : Gilles LAURENT