Problème n°26 : Arithmétique ? Le corrigé
-
Enoncé du problème n° 26
- Calculer en utilisant le tableur $1\times 2\times 3+2$, puis $2\times 3 \times 4+3$, puis $3 \times 4 \times 5+4$, et ainsi de suite jusqu'à $19 \times 20 \times 21+20$.
- Quelle conjecture peut être émise ?
- Cette conjecture est-elle vraie ?
Auteur : Luc GIRAUD

-
Correction du problème n° 26
- Calculer en utilisant le tableur $1\times 2\times 3+2$, puis $2\times 3 \times 4+3$, puis $3 \times 4 \times 5+4$, et ainsi de suite jusqu'à $19 \times 20 \times 21+20$.
- Quelle conjecture peut être émise ?
- Cette conjecture est-elle vraie ?
Auteur : Luc GIRAUD

-
Avec un tableur, on obtient sans peine :
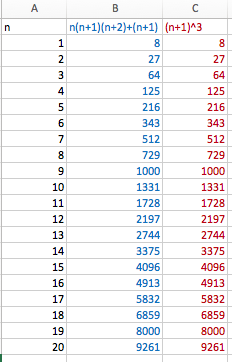
On conjecture alors avec un tableur : pour tout entier naturel $n$: $n(n+1)(n+2)+(n+1)=(n+1)^3$
$$\begin{array}{rl} n(n+1)(n+2)+(n+1)& = (n+1)\left[n(n+2)+1\right] \\ &= (n+1)(n^2+2n+1)\\ &=(n+1)(n+1)^2\\ &= (n+1)^3 \end{array}$$
Conclusion : pour tout entier naturel $n$: $n(n+1)(n+2)+(n+1)=(n+1)^3$



