Problème n° 72, Le problème de la chèvre le corrigé
Maths ...
Problèmes de l'année 2019-2020
Problème n ° 72
Le problème de la chèvre, le corrigé
-
Enoncé du problème n°72
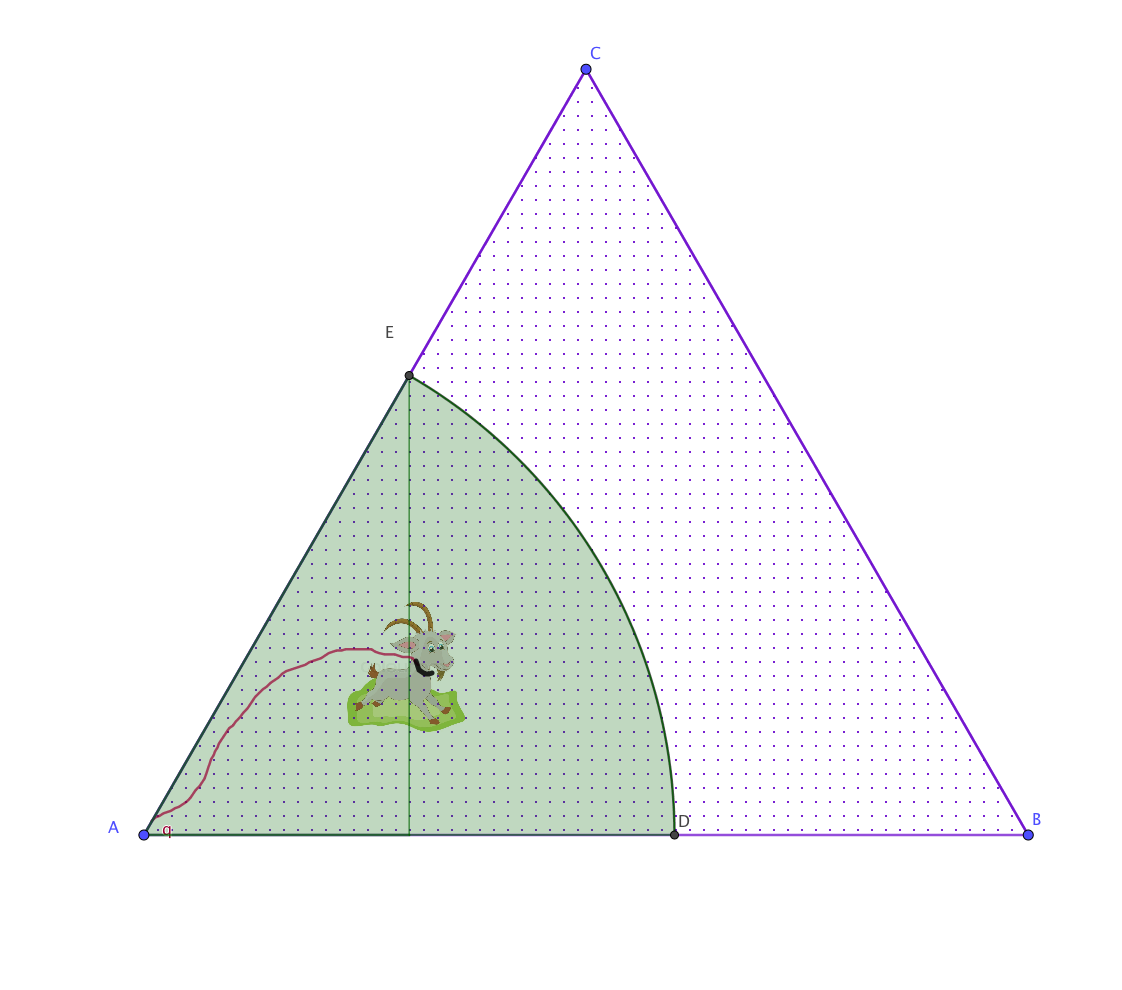
Soit un champ possédant 3 côtés de 100m de long formant un triangle équilatéral.
Soit une chèvre (outil idéal de remplacement de la tondeuse) attachée à un des sommets par une corde.
Quelle doit être la longueur de la corde pour qu'elle puisse brouter exactement la moitié de la surface du pré. -
Correction du problème n°72
L'aire du champ est : $$\text{Aire }(ABC) =\dfrac{\text{Base }\times \text{Hauteur }}{2}$$ $$\text{Aire }(ABC) =100^{2} \times \frac{\sqrt{3}}{4} = 2500\sqrt{3} \approx 4330$$ Soit \(\ell\) la longueur de la corde.
L'aire de la partie pouvant être broutée est : $$\text{Aire broutée }=\ell^{2} \times \frac{\pi}{6}$$ On doit donc résoudre : $$ \ell^{2} \times \frac{\pi}{6}=\frac{2500\sqrt{3}}{2}$$ $$\ell = \sqrt{\frac{7500\sqrt{3}}{\pi}} = \frac{50\times 3^{\frac{3}{4}}}{\sqrt{\pi}}$$ $$\ell \approx 64,3 \text{m}$$
