Maths ...

Problème n ° 73

Echafaudage, le corrigé

• Enoncé du problème n° 73

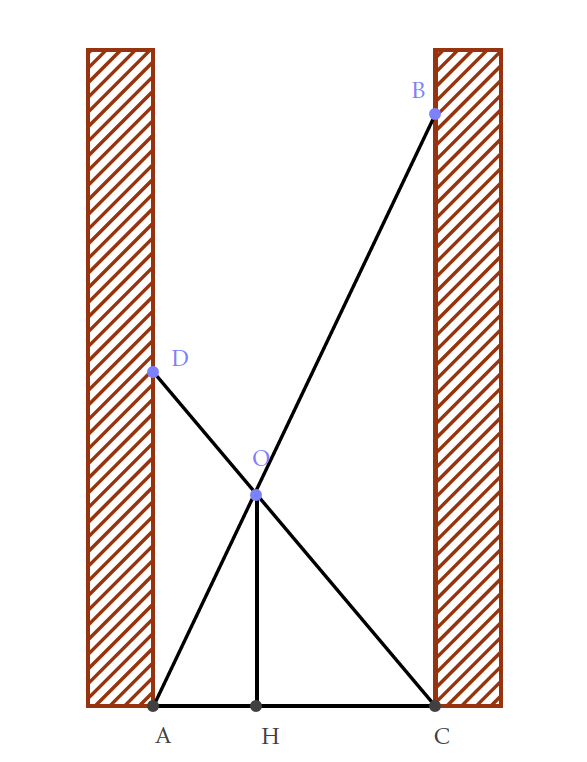
  Deux planches : une grande (AB de trois mètres) et une petite (CD de deux mètres) sont appuyées sur deux murs.
  Elles se croisent à un mètre du sol qui est horizontal.
  Quelle distance sépare les deux murs ?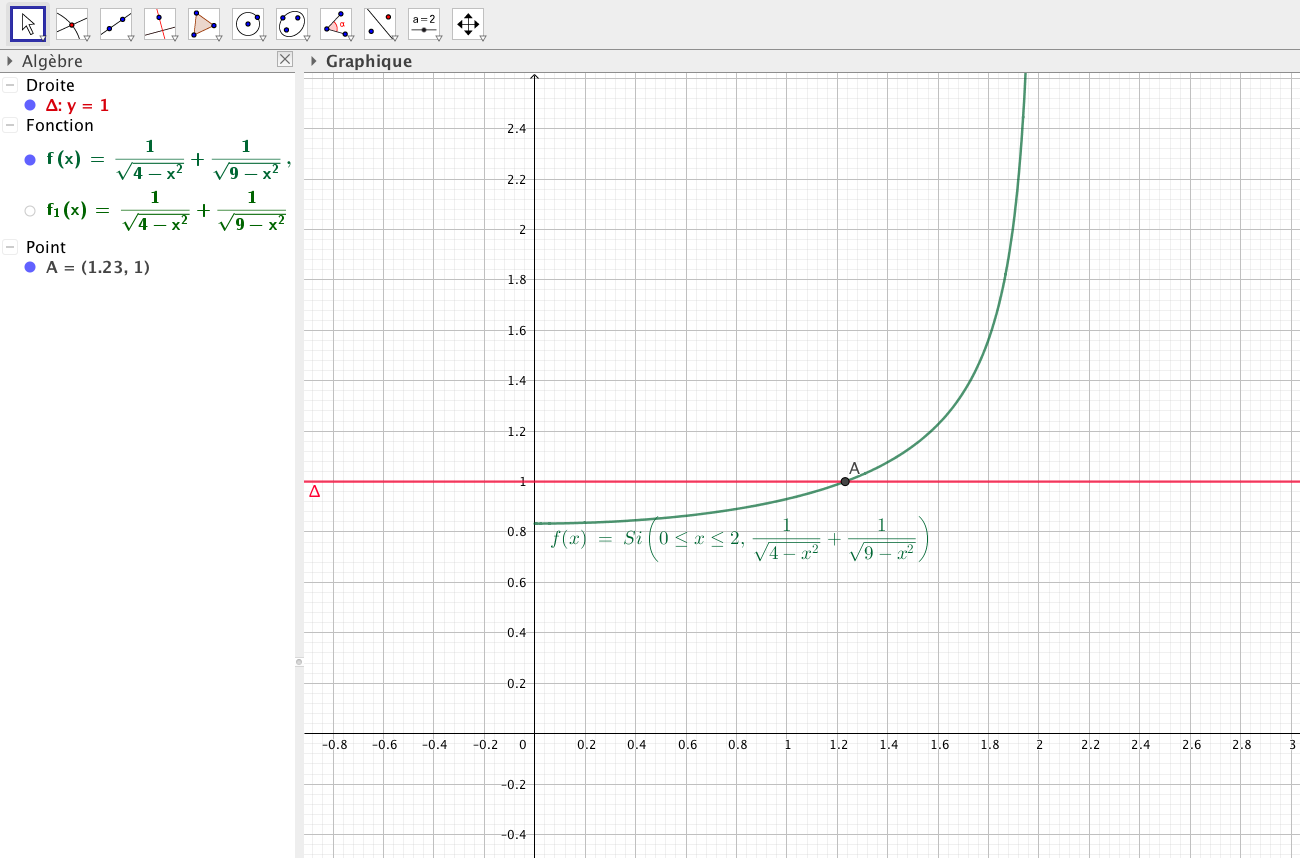

• 

  Correction du problème n°73

  Notons \(x\) la distance cherchée. On utilise d'abord le théorème
  de Thalès qui donne, puisque \(OH = 1\), dans un premier temps
  \(\dfrac{AH}{x}=\dfrac{1}{BC}\) et donc \(AH =\dfrac{x}{BC}\; (1)\) 
  
  
  Puis $$\dfrac{1}{AD}=\dfrac{HC}{x}=\dfrac{x-AH}{x}=1-\dfrac{AH}{x}$$
  on en déduit que $$AH=x-\dfrac{x}{AD}\; (2)$$
  
  De (1) et (2) on tire \(\dfrac{1}{BC}=1-\dfrac{1}{AD} \) soit \(\dfrac{1}{BC}+\dfrac{1}{AD}=1\)
  
  
  Mais comme \(BC =\sqrt{9-x^2}\) et \( AD =\sqrt{4-x^2} \) on obtient au final
  $$ \dfrac{1}{\sqrt{9-x^2}}+\dfrac{1}{\sqrt{4-x^2}}=1$$
  En notant \( f \) la fonction de \( [ 0 ; 2 ]\) dans \( \mathbb R \) telle que \( x \mapsto f(x) = \dfrac{1}{\sqrt{9-x^2}}+\dfrac{1}{\sqrt{4-x^2}} \)
  
  il suffit de résoudre l'équation \( f(x) = 1\).
  
  Le plus simple est d'utiliser un traceur de courbe qui permet de donner une valeur de \( x\) au centimètre près : 1, 23 m
  1, 23 m environ sépare les deux murs.

Luc Giraud

Maths ...

Problème n ° 73

Echafaudage

Luc Giraud

Maths ...

Problème n ° 72

Le problème de la chèvre, le corrigé

• Enoncé du problème n°72

  Soit un champ possédant 3 côtés de 100m de long formant un triangle équilatéral.
  Soit une chèvre (outil idéal de remplacement de la tondeuse) attachée à un des sommets par une corde.
  Quelle doit être la longueur de la corde pour qu'elle puisse brouter exactement la moitié de la surface du pré.

• Correction du problème n°72

  L'aire du champ est : $$\text{Aire }(ABC) =\dfrac{\text{Base }\times \text{Hauteur }}{2}$$ $$\text{Aire }(ABC) =100^{2} \times \frac{\sqrt{3}}{4} = 2500\sqrt{3} \approx 4330$$ Soit \(\ell\) la longueur de la corde.
  L'aire de la partie pouvant être broutée est : $$\text{Aire broutée }=\ell^{2} \times \frac{\pi}{6}$$ On doit donc résoudre : $$ \ell^{2} \times \frac{\pi}{6}=\frac{2500\sqrt{3}}{2}$$ $$\ell = \sqrt{\frac{7500\sqrt{3}}{\pi}} = \frac{50\times 3^{\frac{3}{4}}}{\sqrt{\pi}}$$ $$\ell \approx 64,3 \text{m}$$

Luc Giraud