Maths ...

Problème n ° 105

Les élastiques, le corrigé

• Enoncé du problème n° 105

  $AB$ et $CD$ sont deux pièces de bois verticales sur une surface horizontale $AC$.
  $AD$ est un élastique qui peut être étiré théoriquement aussi loin que vous le souhaitez.
  $BC$ est plus long que $AD$, mais possède les mêmes propriétés.
  $P$ est le point d'intersection des deux élastiques.
  Démontrez que la hauteur $P$ au-dessus de la surface horizontale reste constante peu importe la longueur $AC$ (en supposant que les élastiques restent tendus).
  Dans l'exemple ci-dessus, $AB =$12 cm et $CD =$ 6 cm et je pourrais vous demander la distance constante $PQ$, peu importe la distance que mesure $AC$.

• Correction du problème n°105

  Une solution :
  On se place dans le repère où

  • $A(0,0); B(0,12);C(a,0),D(a,6)$
  • on calcule les coordonnées du point $P$ intersection des droites $(AD)$ et $(BC)$.
    On obtient $(AD): y=\frac{6}{a}x$ et $(BC): y=-\frac{12}{a}x+12$
  • On résout le système $\left\lbrace \begin{array}{l} y=\frac{6}{a}x\\ y=-\frac{12}{a}x+12 \end{array} \right. \iff \left\lbrace \begin{array}{l} y=\frac{6}{a}x\\ \frac{6}{a}x=-\frac{12}{a}x+12 \end{array} \right. \iff \left\lbrace \begin{array}{l} y=\frac{6}{a}\times \frac{ 2}{3}a =4\\ x= \frac{ 2}{3}a \end{array} \right. $
  • On a donc $P( \frac{ 2}{3}a;4)$ et $Q( \frac{ 2}{3}a;0)$ et donc $PQ=4$

  Une animation sous GeoGebra :

   

Luc GIRAUD

Maths ...

Problème n ° 105

Les élastiques

Luc Giraud

Maths ...

Problème n ° 104

Un casse-tête, le corrigé

• Enoncé du problème n° 104

  Un test pour enfants pose problème aux gros cerveaux du W... Ce casse-tête, qui consiste à remplir des cases vides par des chiffres de 1 à 9, a été présenté à des élèves de CE2 dans une classe de Bao Loc, au Vietnam.
  Les chiffres 1 à 9 doivent tous être utilisés !
  Comme le souligne le Guardian, ce problème composé d’opérations simples comme des additions et des multiplications, ne devrait pas en théorie être compliqué à résoudre. Mais selon le professeur Tran Phuong qui l’a proposé à sa classe, cette simplicité n’est qu’apparente : « Il est difficile, même pour des adultes bons en maths ».
  Il a en effet envoyé le casse-tête à son entourage, y compris à un Docteur en économie et mathématiques, mais personne n’a su trouver la réponse… Et vous, y parviendrez-vous ? 
  On vous aide : les deux points représentent le symbole « diviser ».

• Correction du problème n°104

  On peut bien sûr chercher des solutions par tatonnement, ou chercher toutes les solutions avec un script Python.
  Si on note $a,b,c,d,e,f,g,h,i$ les nombres dans l'ordre d'apparition:
  On doit avoir $$a+13\times\dfrac{b}{c} +d+12\times e -f-11+g\times \dfrac{h}{i}-10=66 $$

• Un script Python

  
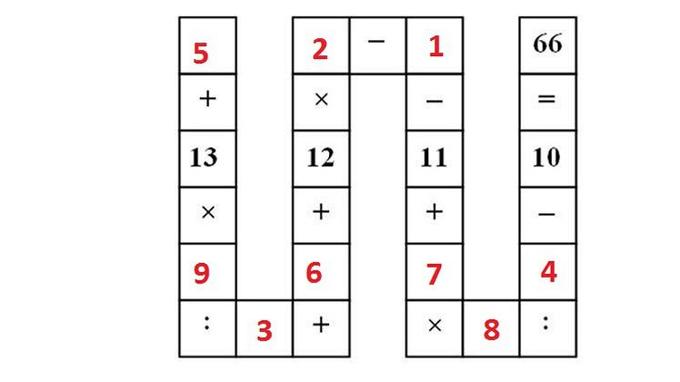
  # Un casse-tête
  import itertools
  Sol=[]
  l=[1,2,3,4,5,6,7,8,9]
  for p in itertools.permutations(l):
      R=p[0]+(13*p[1]/p[2])+p[3]+12*p[4]-p[5]-11+p[6]*p[7]/p[8]-10
      if R==66:
          Sol.append([p[0],p[1],p[2],p[3],p[4],p[5],p[6],p[7],p[8]])
          
  print(Sol)
  

  Et voici la liste des 128 solutions !
  [[1, 2, 6, 4, 7, 8, 3, 5, 9], [1, 2, 6, 4, 7, 8, 5, 3, 9], [1, 3, 2, 4, 5, 8, 7, 9, 6], [1, 3, 2, 4, 5, 8, 9, 7, 6], [1, 3, 2, 9, 5, 6, 4, 7, 8], [1, 3, 2, 9, 5 , 6, 7, 4, 8], [1, 3, 4, 7, 6, 5, 2, 9, 8], [1, 3, 4, 7, 6, 5, 9, 2, 8], [1, 3, 6, 2, 7, 9, 4, 5, 8], [1, 3, 6, 2, 7, 9, 5, 4, 8], [1, 3, 9, 4, 7, 8, 2, 5, 6], [1, 3, 9, 4, 7, 8, 5, 2, 6], [1, 4, 8, 2, 7, 9, 3, 5, 6], [1, 4, 8, 2, 7, 9, 5, 3, 6], [1, 5, 2, 3, 4, 8, 7, 9, 6], [1, 5, 2, 3, 4, 8, 9, 7, 6], [1, 5, 2, 8, 4, 7, 3, 9, 6], [1, 5, 2, 8, 4, 7, 9, 3, 6], [1, 5, 3, 9, 4, 2, 7, 8, 6], [1, 5, 3 , 9, 4, 2, 8, 7, 6], [1, 9, 6, 4, 5, 8, 3, 7, 2], [1, 9, 6, 4, 5, 8, 7, 3, 2], [ 1, 9, 6, 7, 5, 2, 3, 4, 8], [1, 9, 6, 7, 5, 2, 4, 3, 8], [2, 1, 4, 3, 7, 9, 5, 6 , 8], [2, 1, 4, 3, 7, 9, 6, 5, 8], [2, 3, 6, 1, 7, 9, 4, 5, 8], [2, 3, 6, 1, 7, 9, 5, 4, 8], [2, 4, 8, 1, 7, 9, 3, 5, 6], [2, 4, 8, 1, 7, 9, 5, 3, 6], [2, 8, 6, 9, 4, 1, 5, 7, 3], [2, 8, 6, 9, 4, 1, 7, 5, 3], [2, 9, 6, 3, 5, 1, 4, 7, 8], [2 , 9, 6, 3, 5, 1, 7, 4, 8], [3, 1, 4, 2, 7, 9, 5, 6, 8], [3, 1, 4, 2, 7, 9, 6, 5, 8], [3, 2, 1, 5, 4, 7, 8, 9, 6], [3, 2, 1, 5, 4, 7, 9, 8, 6], [3, 2, 4, 8, 5, 1 , 7, 9, 6], [3, 2, 4, 8, 5, 1, 9, 7, 6], [3, 2, 8, 6, 5, 1, 7, 9, 4], [3, 2, 8, 6, 5, 1, 9, 7, 4], [3, 5, 2, 1, 4, 8, 7, 9, 6], [3, 5, 2, 1, 4, 8, 9, 7, 6], [3, 6, 4, 9, 5, 8, 1, 7, 2], [3, 6, 4, 9, 5, 8, 7, 1, 2], [3, 9, 2, 8, 1, 5, 6, 7, 4], [3, 9, 2, 8, 1, 5, 7, 6, 4], [3, 9, 6, 2, 5, 1, 4, 7, 8], [3, 9, 6, 2, 5, 1, 7, 4, 8], [4, 2, 6, 1, 7, 8, 3, 5, 9], [4, 2, 6, 1, 7, 8, 5, 3, 9], [4, 3, 2, 1 , 5, 8, 7, 9, 6], [4, 3, 2, 1, 5, 8, 9, 7, 6], [4, 3, 9, 1, 7, 8, 2, 5, 6], [4, 3, 9, 1, 7, 8, 5, 2, 6], [4, 9, 6, 1, 5, 8, 3, 7, 2], [4, 9, 6, 1, 5, 8, 7, 3, 2 ], [5, 1, 2, 9, 6, 7, 3, 4, 8], [5, 1, 2, 9, 6, 7, 4, 3, 8], [5, 2, 1, 3, 4, 7, 8, 9, 6], [5, 2, 1, 3, 4, 7, 9, 8, 6], [5, 3, 1, 7, 2, 6, 8, 9, 4], [5, 3, 1, 7, 2, 6, 9, 8, 4], [5, 4, 1, 9, 2, 7, 3, 8, 6], [5, 4, 1, 9, 2, 7, 8, 3, 6], [5, 4 , 8, 9, 6, 7, 1, 3, 2], [5, 4, 8, 9, 6, 7, 3, 1, 2], [5, 7, 2, 8, 3, 9, 1, 6, 4] , [5, 7, 2, 8, 3, 9, 6, 1, 4], [5, 9, 3, 6, 2, 1, 7, 8, 4], [5, 9, 3, 6, 2, 1, 8 , 7, 4], [6, 2, 8, 3, 5, 1, 7, 9, 4], [6, 2, 8, 3, 5, 1, 9, 7, 4], [6, 3, 1, 9, 2, 5, 7, 8, 4], [6, 3, 1, 9, 2, 5, 8, 7, 4], [6, 9, 3, 5, 2, 1, 7, 8, 4], [6, 9, 3, 5, 2, 1, 8, 7, 4], [7, 1, 4, 9, 6, 5, 2, 3, 8], [7, 1, 4, 9, 6, 5, 3, 2, 8], [7, 2, 8, 9, 6, 5, 1, 3, 4], [7, 2, 8, 9, 6, 5, 3, 1, 4], [7, 3, 1, 5, 2, 6, 8, 9, 4], [7, 3, 1, 5, 2, 6, 9, 8, 4], [7, 3, 2, 8, 5, 9, 1, 6, 4], [7, 3, 2, 8, 5 , 9, 6, 1, 4], [7, 3, 4, 1, 6, 5, 2, 9, 8], [7, 3, 4, 1, 6, 5, 9, 2, 8], [7, 5, 2, 8, 4, 9, 1, 3, 6], [7, 5, 2, 8, 4, 9, 3, 1, 6], [7, 6, 4, 8, 5, 9, 1, 3, 2], [7, 6, 4, 8, 5, 9, 3, 1, 2], [7, 9, 6, 1, 5, 2, 3, 4, 8], [7, 9, 6, 1, 5, 2, 4, 3, 8], [8, 2, 4, 3, 5, 1, 7, 9, 6], [8, 2, 4, 3, 5, 1, 9, 7, 6], [8, 3, 2, 7, 5, 9, 1, 6, 4], [8, 3, 2, 7, 5, 9, 6, 1, 4], [8, 5, 2, 1, 4, 7, 3, 9, 6], [8, 5, 2 , 1, 4, 7, 9, 3, 6], [8, 5, 2, 7, 4, 9, 1, 3, 6], [8, 5, 2, 7, 4, 9, 3, 1, 6], [ 8, 6, 4, 7, 5, 9, 1, 3, 2], [8, 6, 4, 7, 5, 9, 3, 1, 2], [8, 7, 2, 5, 3, 9, 1, 6 , 4], [8, 7, 2, 5, 3, 9, 6, 1, 4], [8, 9, 2, 3, 1, 5, 6, 7, 4], [8, 9, 2, 3, 1, 5, 7, 6, 4], [9, 1, 2, 5, 6, 7, 3, 4, 8], [9, 1, 2, 5, 6, 7, 4, 3, 8], [9, 1, 4, 7, 6, 5, 2, 3, 8], [9, 1, 4, 7, 6, 5, 3, 2, 8], [9, 2, 8, 7, 6, 5, 1, 3, 4], [9 , 2, 8, 7, 6, 5, 3, 1, 4], [9, 3, 1, 6, 2, 5, 7, 8, 4], [9, 3, 1, 6, 2, 5, 8, 7, 4], [9, 3, 2, 1, 5, 6, 4, 7, 8], [9, 3, 2, 1, 5, 6, 7, 4, 8], [9, 4, 1, 5, 2, 7 , 3, 8, 6], [9, 4, 1, 5, 2, 7, 8, 3, 6], [9, 4, 8, 5, 6, 7, 1, 3, 2], [9, 4, 8, 5, 6, 7, 3, 1, 2], [9, 5, 3, 1, 4, 2, 7, 8, 6], [9, 5, 3, 1, 4, 2, 8, 7, 6], [9, 6, 4, 3, 5, 8, 1, 7, 2], [9, 6, 4, 3, 5, 8, 7, 1, 2], [9, 8, 6, 2, 4, 1, 5, 7, 3], [9, 8, 6, 2, 4, 1, 7, 5, 3]]

Luc GIRAUD