Enoncé de l'énigme n° 4 (Lycée 1)

Un examen est composé de 24 questions.
Le barème est le suivant :

• 0 s'il n'y a pas de réponse,
• 1 point si la réponse est juste
• et -0,25 point si la réponse est incorrecte.

Un étudiant a obtenu 13 points. Quel est le maximum de réponses justes qu'il a pu donner ?

Correction de l'énigme n° 4 (Lycée 1)

Dans les conditions de l'énoncé, pour obtenir 13 points, l'étudiant a au moins donné 13 bonnes réponses.
On note $x$ le nombre de bonnes réponses de l'étudiant.
$y$ le nombre de réponses fausses.
On cherche le maximum de $x$ sachant que l'on a les contraintes : $$13\leq x\leq 24$$ $$0\leq y\leq 24$$ $$x-\frac{1}{4}y=13$$ On cherche donc un point à coordonnées entières sur la droite $\Delta$ d'équation $x-\frac{1}{4}y=13$, appartenant au carré défini par les inégalités $\left\lbrace \begin{array}{l} 0\leq x \leq 24\\ 0\leq y \leq 24 \end{array} \right.$
On peut représenter la situation de la façon suivante :

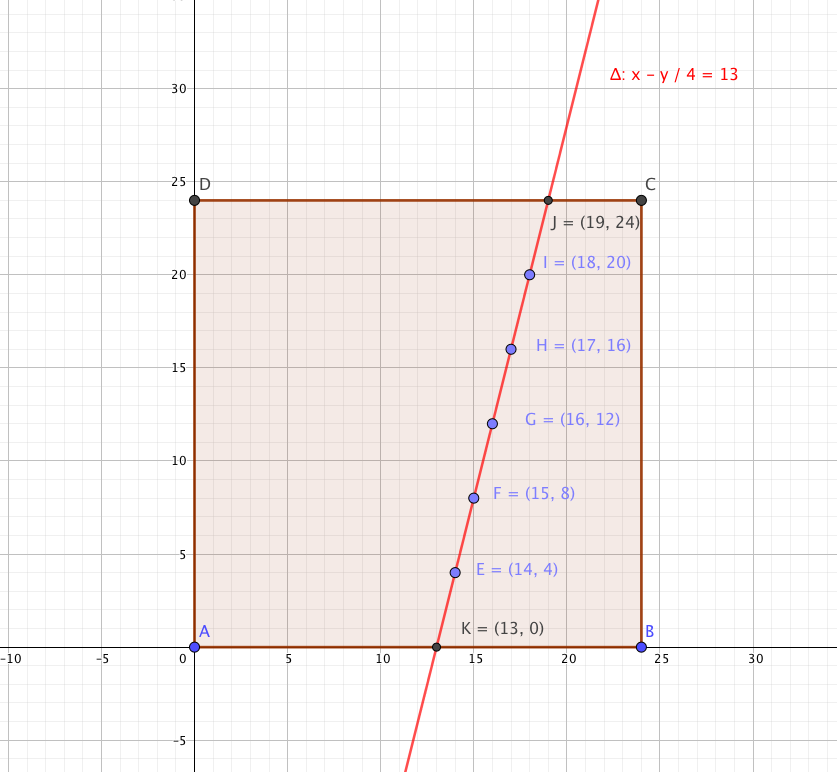
Parmi les 7 points obtenus, on prend en compte que les 3 premiers : $(13;0);(14;4);(15;8)$.
En effet le nombre de questions est 24; donc $x+y\leq 24$.

Auteur : Luc GIRAUD

Enoncé de l'énigme n° 3 (Lycée 1)

La grande base d'un trapèze a pour longueur 15 cm et le segment joignant les milieux de ses diagonales mesure 3 cm.
Quelle est la longueur de la petite base de ce trapèze ?

Correction de l'énigme n° 3 (Lycée 1)

Appelons $ABCD$ le trapèze, $[DC]$ est sa grande base et $[AB]$ est donc sa petite base.
Appelons aussi $I$ le milieu de la diagonale $[AC]$, $J$ celui de la diagonale $[BD]$ et $K$ l'intersection de $[AC]$ et $[BD]$.
Montrons que le segment $[IJ]$ est parallèle à $(DC)$ ( et donc à $(AB)$)
Considérons la droite perpendiculaire à $(DC)$ et $(AB)$ et passant par le point $I$ . Cette droite coupe $(AB)$ en $I_1$ et $(CD)$ en $I_2$

On montre en utilisant le théorème de Thalès(figure 2) que $\frac{II_1}{II_2}=\frac{IA}{IC}= 1$
(on rappelle que I est le milieu de $[AC]$) le point $I$ est donc le milieu de $I_1I_2$ et est à égale distance des droites $(AB)$ et $(CD)$
On montre de même que $J$ est à égale distance des droites $(AB)$ et $(CD)$.
On en déduit alors que la droite $(IJ)$ est parallèle à $(DC)$ ( et donc à $(AB)$
On applique maintenant le théorème de Thalès dans les triangles $KDC$ et $KIJ$ ($(IJ)//(DC)$)
On trouve $\frac{IJ}{DC} =\frac{KI}{KD}$ donc $\frac{KI}{KD}=\frac{1}{5}$
On en déduit que $KI$ est quatre fois plus grand que $ID$ et comme $ID=IB$
on en déduit aussi que $NB$ est trois fois plus grand que $NB$
Si on applique maintenant le théorème de Thalès dans les triangles $KIJ$ et $KAB$, on trouve $\frac{IJ}{AB} = \frac{KI}{KD}$
soit $\frac{3}{AB}= \frac{1}{3}$ et donc $AB= 9$

Auteur : Alexandre GROLLIER

Enoncé de l'énigme n° 5 (Lycée 1)

Si ABCD est un carré de côté 3 cm, quelle est l'aire de la région coloriée ?

Correction de l'énigme n° 3 (Lycée 2)

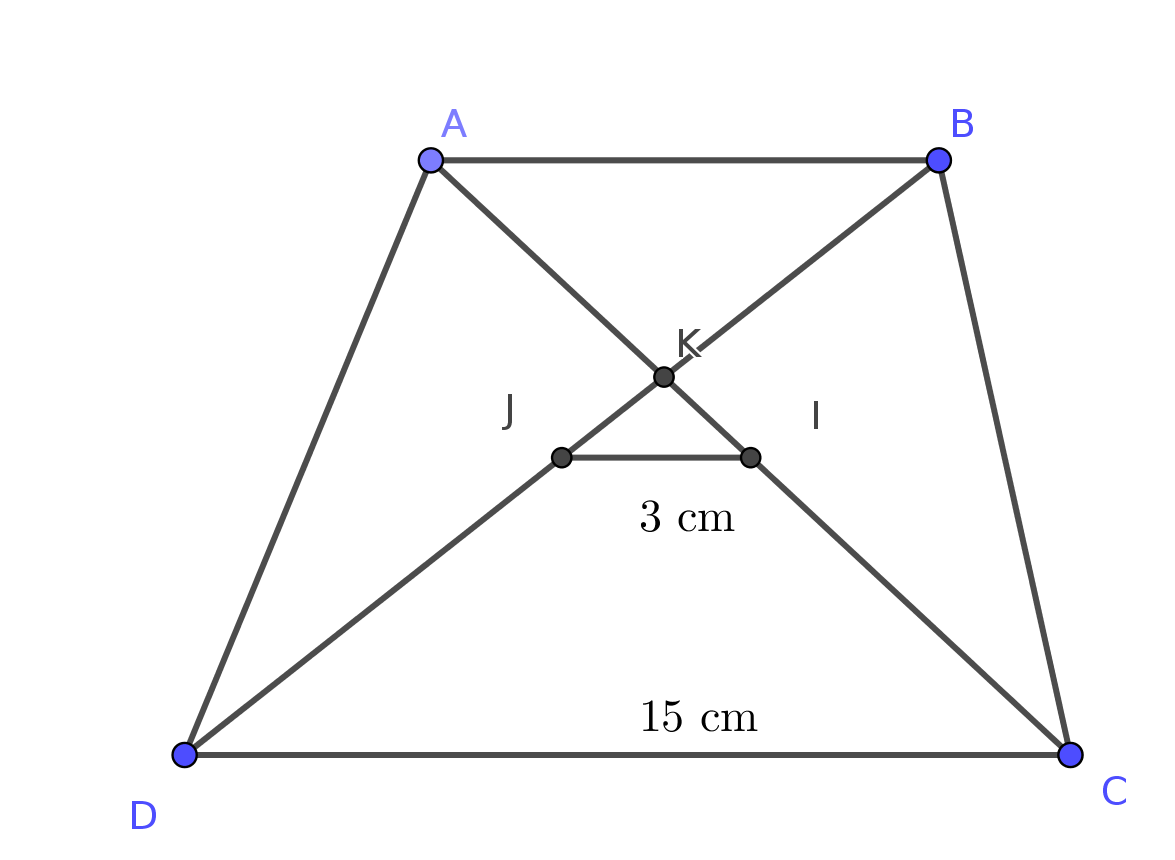
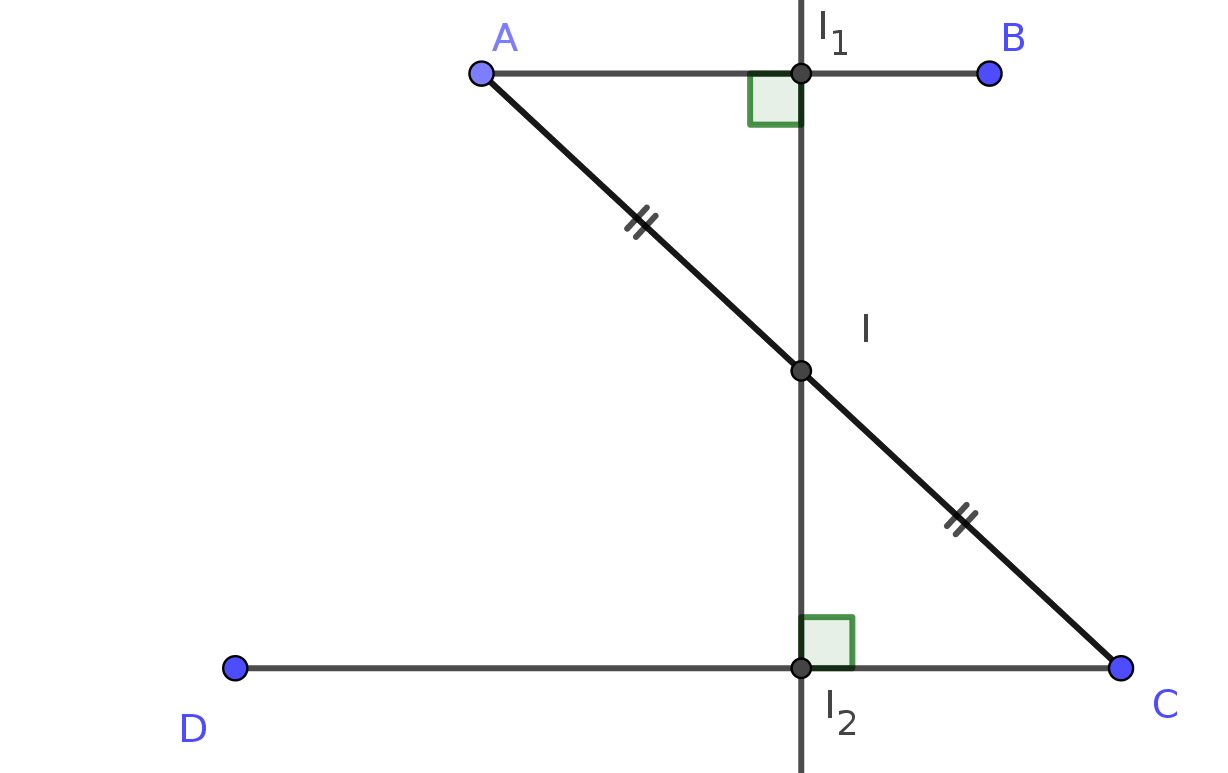
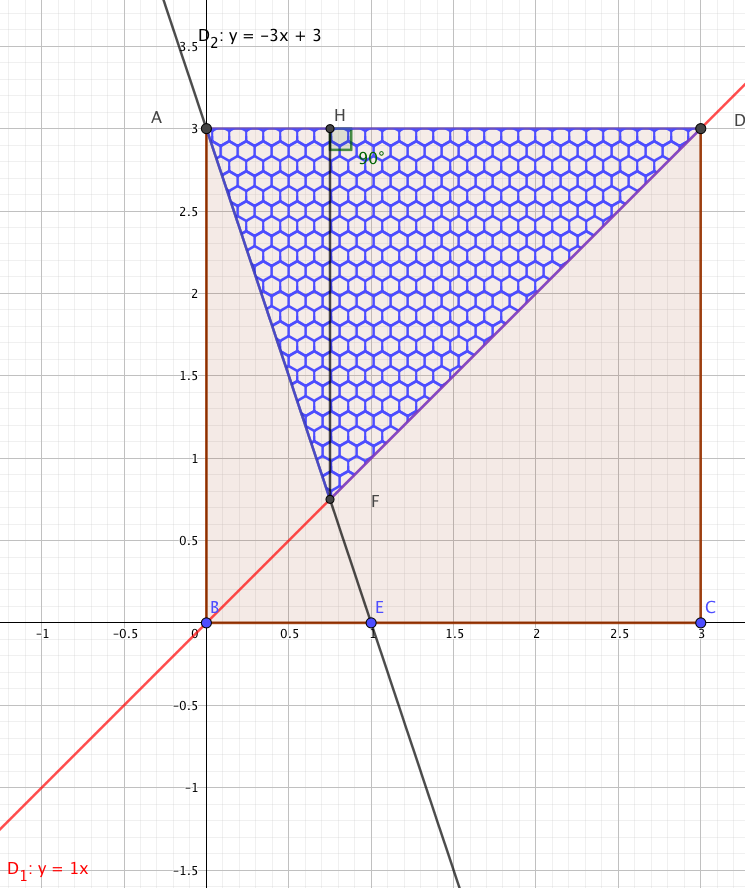Avec les notations de la figure ci-dessus, l'aire du triangle FAD vaut : $\mathcal{A}= \dfrac{AD\times FH}{2}= \dfrac{3}{2}FH$.
Calulons alors les cooronnées de $H$, point se trouvant à l'intersection des droites $(BD)$ et $(AE)$.

• Equation de $(BD)$:
  cette droite passe par l'origine O et a pour coeffifficient directeur 1.
  Ainsi (BD): $y=x$
• Equation de $(AE)$:
  son coefficient directer est -3.
  et a pour équation réduite : $y-y_A= m(x-x_A)$, soit $y-3=-3(x-0)$
  Ainsi (AE): $y=-3x+3$
• Coordonnées de H: $$\left\lbrace \begin{array}{l} y=x\\ y=-3x+3 \end{array} \right.\iff \left\lbrace \begin{array}{l} y=x\\ x=-3x+3 \end{array} \right. \iff \left\lbrace \begin{array}{l} y=x\\ x=\frac{3}{4} \end{array} \right.\iff \left\lbrace \begin{array}{l} y=\frac{3}{4}\\ x=\frac{3}{4} \end{array} \right.$$ Ainsi $H\left( \dfrac{3}{4}; \dfrac{3}{4}\right) $.
• Alors $FH= 3- \dfrac{3}{4}= \dfrac{9}{4}$, puis l'aire coloriée vaut $\mathcal{A}= \dfrac{3}{2}\times \dfrac{9}{4}= \dfrac{27}{8} $.

Auteur : Luc Giraud