Un problème ...

Pour se divertir

La solution la semaine suivante !

proposé par l'équipe de maths

du lycée l'Oiselet

Enoncé de l'énigme n° 5 (Lycée 2)

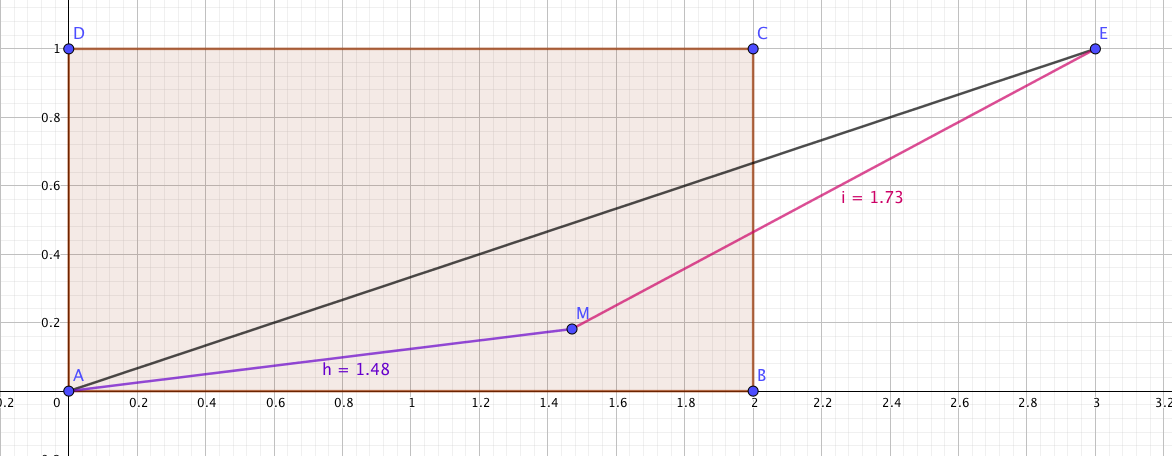
Si l'on choisit un point P dans un plan, muni d'un repère orthonormé, contenu dans un rectangle dont les sommets sont les points de coordonnées (0,0), (2,0), (2,1) et (0,1).
Quelle est la probabilité que P soit plus proche de l'origine que du point de coordonnées (3,1) ?

Correction de l'énigme n° 5 (Lycée 2)

Une première approche ?

On peut par exemple utiliser une démarche algorithmique :

Une éxécution de ce script fournit :

 Ma valeur expérimentale de la probabilite de U est 0.7523

Théorème Soient $A$ et $B$ deux points distincts,$\Delta$ la médiatrice de $[AB]$, $\mathcal{P}_A$,(resp. $\mathcal{P}_B$)le demi-plan ouvert de frontière $\Delta$ contenant $A$ (resp. $B$). Alors
$$M\in \Delta \Rightarrow MA=MB.$$ $$M\in \mathcal{P}_A \Rightarrow MA<MB.$$ $$M\in \mathcal{P}_B \Rightarrow MA>MB.$$

On peut illustrer cette propriété de la façon suivante :Cocher activer la trace

Preuve: Notons $s$ la réflexion d'axe $\Delta$, on a donc $s(A)=B$. Si $M\in \Delta$ alors $MA=s(M)s(A)=MB$ puisque la réflexion $s$ conserve les distances.
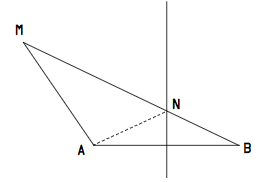
Si $M\in \mathcal{P}_A$ notons $N$ l'intersection du segment $[BM]$ et de $\Delta$ (elle existe car $M$ et $B$ n’appartiennent pas au même demi-plan de frontière $\Delta$.)
Comme $N\notin [MA]$ et $N\in \Delta$ ,on peut écrire $MA < MN+ NA = MN+NB= MB$ (cf.Figure ci-dessous).
Si $M\in \mathcal{P}_B$ on raisonne de la même façon.

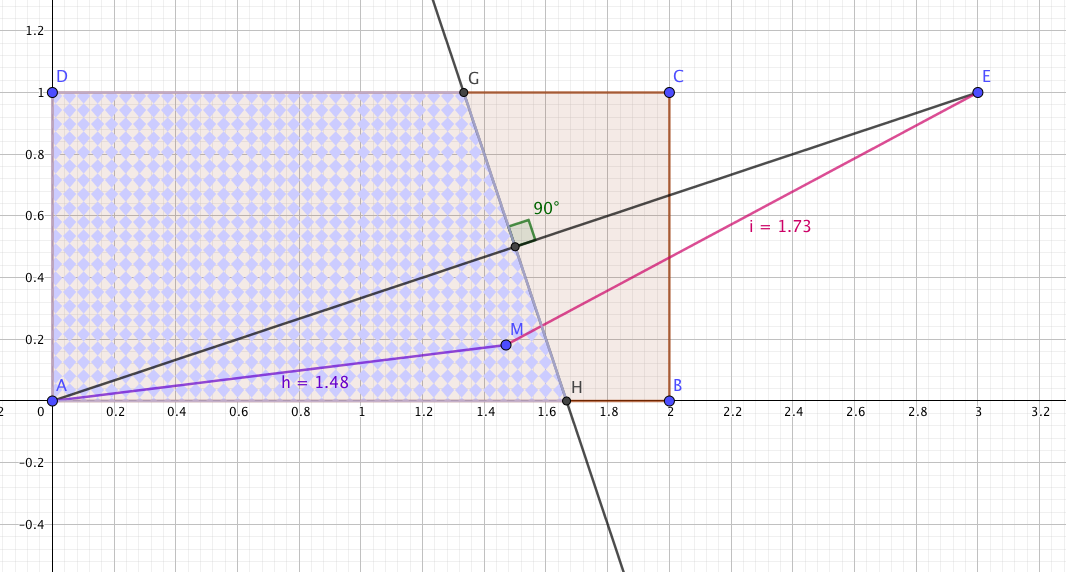On peut commencer par signaler un théorème permettent un régionnement du plan:
On met alors en place le modèle:

• On choisit un point M au hasard, à l'intérieur du rectagle ABCD.
• On note U l'événement :" Le point M est plus proche de A (0,0) que du point E(3,1)."
• On trace la médiatrice $\Delta$ du segment [AE]
• $\Delta$ coupe [AB] et [CD] respectivement en H et G.
• $$\begin{array}{rl} M\in U &\iff MA< ME \\ & \iff M\in \mathcal{P}_A \text{ et } M\in V \\ &\iff M\text{ est à l'intérieur de } AHGD \end{array}$$
• On a $p(U)=\dfrac{\text{ Aire}(U)}{\text{ Aire}(ABCD)}$
• Déterminons une équation de $\Delta$: $$\begin{array}{rl} M \begin{pmatrix} x\\ y\\ \end{pmatrix} \in \Delta &\iff MA= ME \\ & \iff MA^2 = ME^2 \\ &\iff (x-0)^2+(y-0)^2= (x-3)^2+(y-1)^2\\ &\iff x^2+y^2=x^2-6x+9+y^2-2y+1\\ &\iff -6x-2y+10=0\\ &\iff y=5-3x\\ \end{array}$$ $$\begin{array}{rl} H \begin{pmatrix} x\\ 0\\ \end{pmatrix} \in \Delta &\iff 0= 5-3x\\ &\iff x = \frac{5}{3}\\ \end{array}$$ Ainsi $H \begin{pmatrix} \frac{5}{3}\\ 0\\ \end{pmatrix}$ $$\begin{array}{rl} G \begin{pmatrix} x\\ 1\\ \end{pmatrix} \in \Delta &\iff 1= 5-3x\\ &\iff x = \frac{4}{3}\\ \end{array}$$ Ainsi $G \begin{pmatrix} \frac{4}{3}\\ 0\\ \end{pmatrix}$
• L'aire du trapèze AHGD vaut $$\begin{array}{rl} \mathcal{A}&= \dfrac{\left( \text{Grande Base + Petite Base}\right) \times \text{Hauteur}}{2} \\ & \dfrac{(AH+DG)\times AD}{2}\\ &= \dfrac{\left( \frac{5}{3}+\frac{4}{3}\right )\times 1}{2}\\ &= \frac{3}{2} \end{array}$$
• Ainsi $p(U)=\dfrac{\text{ Aire}(U)}{\text{ Aire}(ABCD)}= \dfrac{ \frac{3}{2} }{2}= \frac{3}{4}$

Auteur : Luc GIRAUD