Problème n°1 : Des petits carrés ... ! Le corrigé
-
Enoncé du problème n° 1
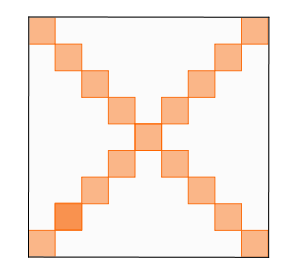
Dans un carré de côté $c=2017$ les carrés de côté 1 sur les diagonales sont coloriés (la figure montre la situation avec $c=9$).
Combien mesure la surface restée blanche ?
Auteur : Luc GIRAUD
-
Correction du problème n° 1
Dans un carré de côté $c=2017$ les carrés de côté 1 sur les diagonales sont coloriés (la figure montre la situation avec $c=9$).
Combien mesure la surface restée blanche ?
Auteur : Luc GIRAUD
- Dans un carré de côté $2017$, il y a $2017^2$ petits carrés de côté 1.
- Il faut donc enlever les carrés oranges des deux diagonales. Il y en a : $2017+2016$.
- Il y a donc : $2017^2-(2017+2016)$ petits carrés blancs.
On peut alors remarquer que : $$\begin{array}{rl} 2017^2-(2017+2016)&= 2017^2-(2017+2017-1) \\ & =2017-2\times 2017+1\\ &=(2017-1)^2\\ &=2016^2 \end{array}$$ On a utilisé le produit remarquable : $$a^2-2ab+b^2=(a-b)^2$$ Une autre piste ?
Analysez la figure ci-dessous :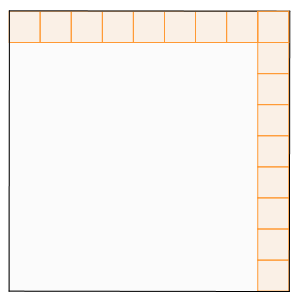
Il y a donc $4 064 256$ petits carrés blancs dans un carré de côté 2017 !
