Maths ...

ABCD est un carré de côté 1, (Q) est un quart de cercle de centre C et passant par B et D.
M est un point variable du segment [AB] distinct de A et B. Par le point M on trace la tangente à (Q) qui coupe le côté [AD] en N. Le point de contact de la tangente avec (Q) est nommé T.
On pose AM = $x$ et AN = $y$ avec $0<x <1$ et $0<y <1$.

1. 1. Démontrer les deux expressions de MN : $$\left\lbrace \begin{array}{l} \text{MN}= \sqrt{x^2+y^2}~\\ \text{MN}= 2-x-y \end{array} \right.$$
   2. En déduire que $y=2+\dfrac{2}{x-2}$
2. En déduire la valeur de $x$ pour laquelle la distance MN est minimale. Quelle est alors cette distance ?
3. En déduire la valeur de $x$ pour laquelle l’aire du triangle AMN est maximale. Quelle est alors cette aire ?

ABCD est un carré de côté 1, (Q) est un quart de cercle de centre C et passant par B et D.
M est un point variable du segment [AB] distinct de A et B. Par le point M on trace la tangente à (Q) qui coupe le côté [AD] en N. Le point de contact de la tangente avec (Q) est nommé T.
On pose AM = $x$ et AN = $y$ avec $0<x <1$ et $0<y <1$.

1. 1. Démontrer les deux expressions de MN : $$\left\lbrace \begin{array}{l} \text{MN}= \sqrt{x^2+y^2}~\\ \text{MN}= 2-x-y \end{array} \right.$$ Dans le triangle AMN rectangle en A; on a d'après Pythagore : $\text{MN}^2 = \text{AM}^2 + \text{AN}^2= x^2+y^2$
      Ainsi $\text{MN}= \sqrt{x^2+y^2}$.
      En appliquant le théorème de Pythagore dans les triangles rectangles CTN et CDN, on a :
      • $\text{CN}^2 = \text{CT}^2 + \text{TN}^2$ donc $\text{TN}^2 = \text{CN}^2- \text{CT}^2$
      • $\text{CN}^2 = \text{CD}^2 + \text{DN}^2$ donc $\text{DN}^2 = \text{CN}^2- \text{CD}^2$
      Mais $\text{CN}= \text{CD}=1$ donc $$\begin{array}{rl} \text{TN}^2 & = \text{CN}^2- \text{CT}^2 \\ & = \text{CN}^2- \text{CD}^2\\ &= \text{DN}^2 \end{array}$$ On a donc $\text{TN}=\text{DN}= \text{DA}-\text{AN}=1-\text{AN}=1-y$
      On prouve de même $\text{TM}=\text{AM}= 1-x$ Il s'en suit : $$\text{MN}=\text{MT}+ \text{TN} =1-x+1-y=2-x-y$$
   2. En déduire que $y=2+\dfrac{2}{x-2}$
      On amontré $\text{MN}^2 = x^2+y^2$ et $\text{MN}^2 =(2-x-y)^2$
      Donc $$\begin{array}{rl} x^2+y^2=(2-x-y)^2& \iff x^2+y^2= 4+x^2+y^2-4x-4y+2xy\\ & \iff 4-4x-4y+2xy = 0\\ &\iff 2xy-4y= 4x-4\\ &\iff y(2x-4)=4x-4\\ &\iff y=\dfrac{4x-4}{2x-4}\\ &\iff y=\dfrac{4x-8+4}{2x-4}\\ &\iff y=\dfrac{4x-8 }{2x-4}+\dfrac{4 }{2x-4}\\ &\iff y= 2+\dfrac{2}{x-2} \end{array}$$
2. En déduire la valeur de $x$ pour laquelle la distance MN est minimale. Quelle est alors cette distance ?
   La distance $MN$ est minimale lorsque $MN^2$ est minimale.
   Notons $\phi : x\mapsto MN^2= x^2+y^2= 2-x-y=2-x-\left ( 2+\dfrac{2}{x-2} \right ) = -x-\dfrac{2}{x-2}$.
   On étudie les variations de $\phi$ sur l'intervalle $[0;1]$:
   • Dérivée : $\phi '(x)=-1+\dfrac{2}{(x-2)^ 2}= \dfrac{2-(x-2)^ 2}{(x-2)^ 2}= \dfrac{\left (\sqrt 2 +x-2\right ) \left (\sqrt 2 -x+2\right )}{(x-2)^ 2}$
   • Signe de la dérivée :
     Sur l'intervalle $[0;1]$, on a : $x\leq 1$ donc $-x\geq -1$ puis $2+\sqrt 2-x\geq 1+\sqrt 2> 0$ $\left.\begin{array}{l} 2+\sqrt 2-x >0 \\ (x-2)^2> 0 \end{array}\right\} \quad \text{ Donc } \phi'(x) \text{ a le signe de } \sqrt 2 +x-2$
   $\phi'(x)= 0 \iff \sqrt 2 +x-2 = 0\iff x= 2-\sqrt 2$
   $\phi'(x) > 0 \iff \sqrt 2 +x-2 > 0\iff x> 2-\sqrt 2$
   On déduit le tableau de variations de $\phi$ sur $[0;1]$: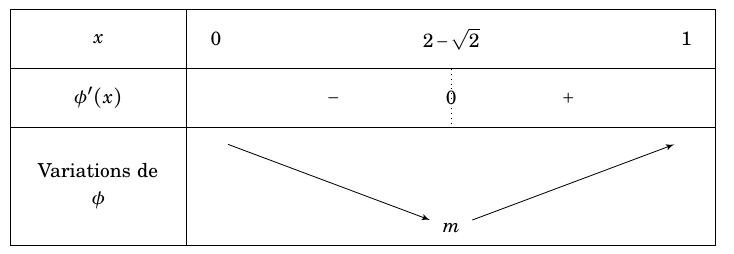
   où $m=\phi(2-\sqrt 2)= -2+\sqrt 2 -\dfrac{2}{2-\sqrt 2-2}= -2+2\sqrt 2$
   

    

3. En déduire la valeur de $x$ pour laquelle l’aire du triangle AMN est maximale. Quelle est alors cette aire ?
   • Première méthode : l'aire de AMN est $$\begin{array}{rl} f(x)&= \dfrac{1}{2}xy\\ & = \dfrac{1}{2}x\left ( 2+\dfrac{2}{x-2}\right ) \\ &= \dfrac{x^2-x}{x-2} \end{array}$$ Sa dérivée est $f'(x)= \dfrac{(2x-1)(x-2)-1(x^2-x)}{(x-2)^2} = \dfrac{ x^2-4x+2}{(x-2)^2}$
     Comme le dénominateur est un carré, la dérivée a le signe du trinôme $x^2-4x+2$.
     $\Delta= b^2-4ac=16-4\times 2= 8$ $$\begin{array}{rrll} x_1&=\dfrac{-b+\sqrt {\Delta}}{2a} &x_2&= \dfrac{-b+\sqrt {\Delta}}{2a}\\ & = \dfrac{4+2\sqrt 2}{2}&&=\dfrac{4-2\sqrt 2}{2}\\ &= 2+\sqrt 2&&=2-\sqrt 2 \end{array}$$ $x^2-4x+2$ est un trinôme du second degré qui a pour racines $x_1$ et $x_2$; il a donc le signe de $a=1$ à l'extérieur des racines et celui de $-a$ à l'intérieur.
     
     On en déduit le tableau de variations de $f$ sur l'intervalle [0;1] :
     
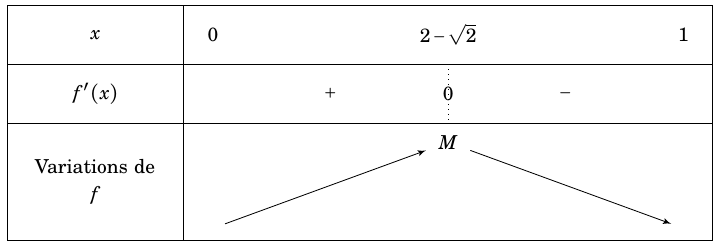
     L'aire du triangle AMN est donc maximale lorsque $x=2-\sqrt 2$. Le maximum de l'aire est $$M=f(2-\sqrt 2)= \dfrac{(2-\sqrt 2)^2-(2-\sqrt 2}{2-\sqrt 2-2}= \dfrac{4+2-4\sqrt 2 - 2+\sqrt 2 }{ -\sqrt 2 }= \dfrac{4-3\sqrt 2 }{ -\sqrt 2 }= \dfrac{6-4\sqrt 2 )}{ 2 }= 3-2\sqrt 2$$
   • Si on souhaite le déduire de la question précédente, $$\begin{array}{rl} \text{Aire}(AMN)&=\text{Aire}(ABCD)-\text{Aire}(CDNT)-\text{Aire}(CBMT)\\ & =1-2\text{Aire}(CMN)\\ &=1-CT\times MN\\ &=1-MN \end{array}$$ L'aire du triangle AMN est donc maximale lorsque la longueur MN est minimale, c'est-à-dire pour $x=2-\sqrt 2$. Le maximum de l'aire est $1- (-2+2\sqrt 2) =3-2\sqrt 2$.