Enoncé du problème n° 53
Ci dessous est représenté dans un repère l’ensemble des points dont le couple \((x,y)\) de coordonnées vérifie la relation \(x^2 — 2y^2 = 1\).
On s’intéresse plus particulièrement aux points de cette courbe dont les coordonnées sont des entiers comme par exemple le point A dont le couple de coordonnées est (1 , 0).
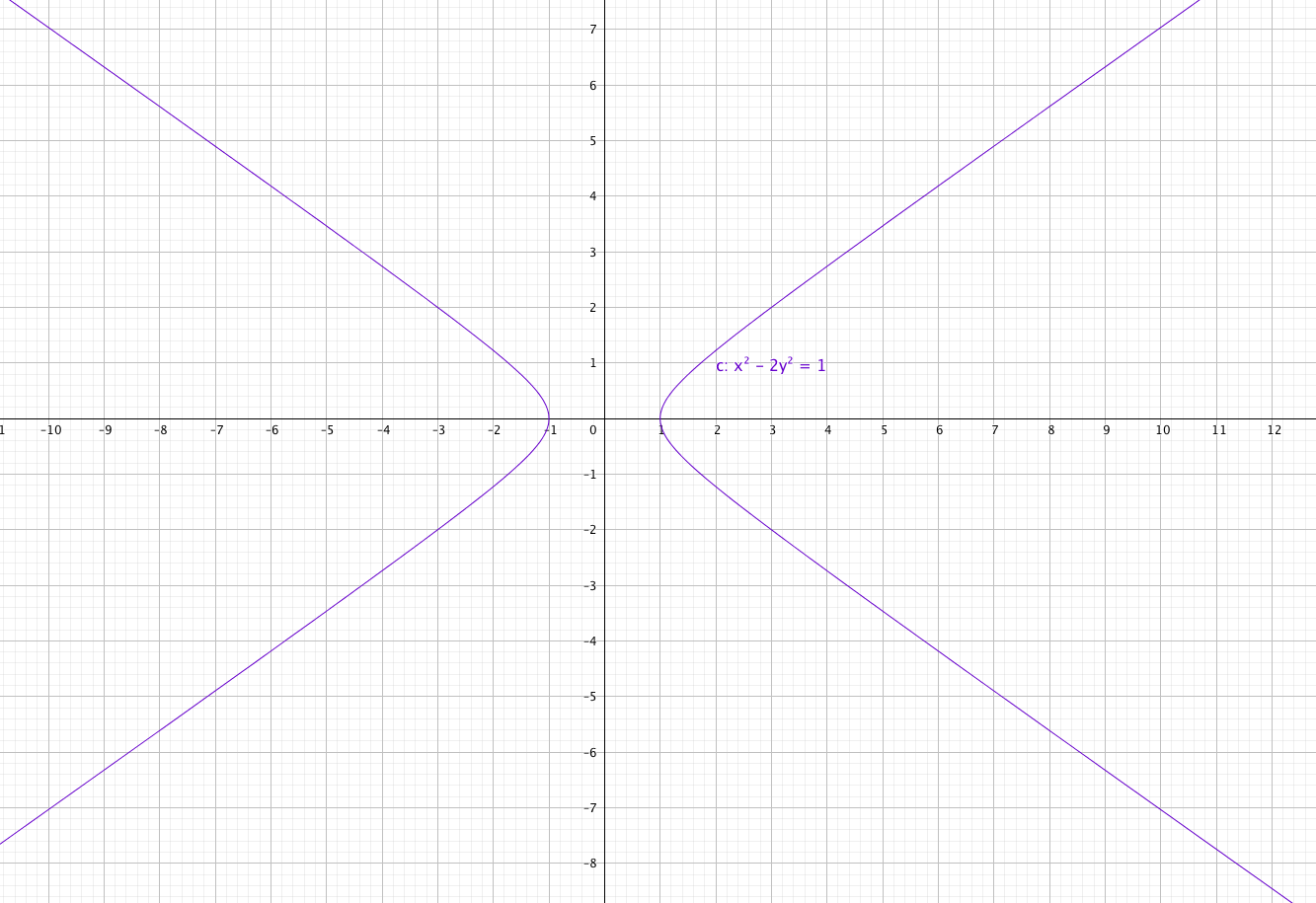
- Donner quatre autres couples d’entiers \((x,y)\) tels que \(x^2 — 2y^2 = 1\).
- Soit \(a\) et \(b\) des entiers naturels. On pose \(A = a + 2b\) et \(B = a + b\).
Exprimer \(A^2 — 2B^2\) en fonction de \(a^2 — 2b^2\).
Donner un nouveau couple d’entiers \((x, y)\) solution de l’équation \(x^2 - 2y^2 = 1 \) tel que \(x > 10\).
- Rédiger un algorithme affichant le premier couple d’entiers \((x, y)\) solution de l’équation \(x^2 — 2y^2 = 1 \) et tel que \(x > 2 018\).
Quel est le couple obtenu?