Enoncé de l'énigme n° 3 (Lycée 1)

La grande base d'un trapèze a pour longueur 15 cm et le segment joignant les milieux de ses diagonales mesure 3 cm.
Quelle est la longueur de la petite base de ce trapèze ?

Correction de l'énigme n° 3 (Lycée 1)

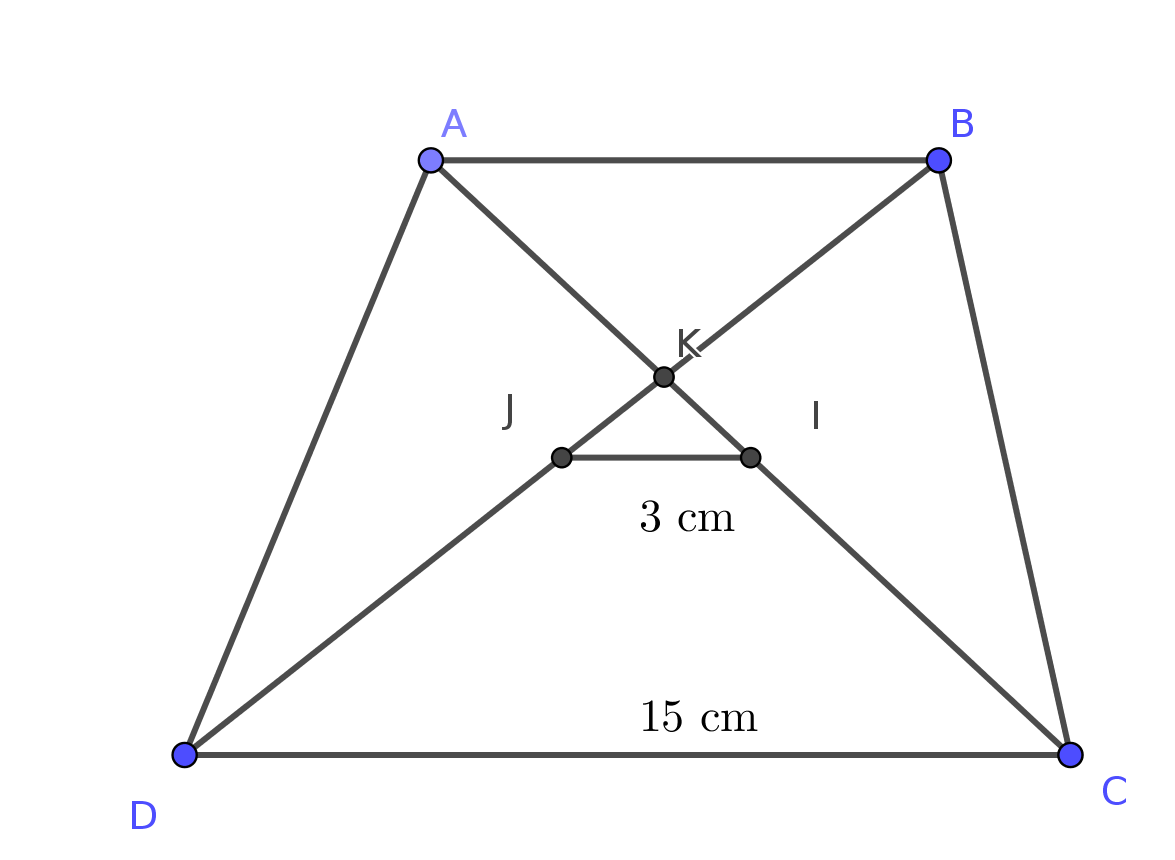
Appelons $ABCD$ le trapèze, $[DC]$ est sa grande base et $[AB]$ est donc sa petite base.
Appelons aussi $I$ le milieu de la diagonale $[AC]$, $J$ celui de la diagonale $[BD]$ et $K$ l'intersection de $[AC]$ et $[BD]$.
Montrons que le segment $[IJ]$ est parallèle à $(DC)$ ( et donc à $(AB)$)
Considérons la droite perpendiculaire à $(DC)$ et $(AB)$ et passant par le point $I$ . Cette droite coupe $(AB)$ en $I_1$ et $(CD)$ en $I_2$

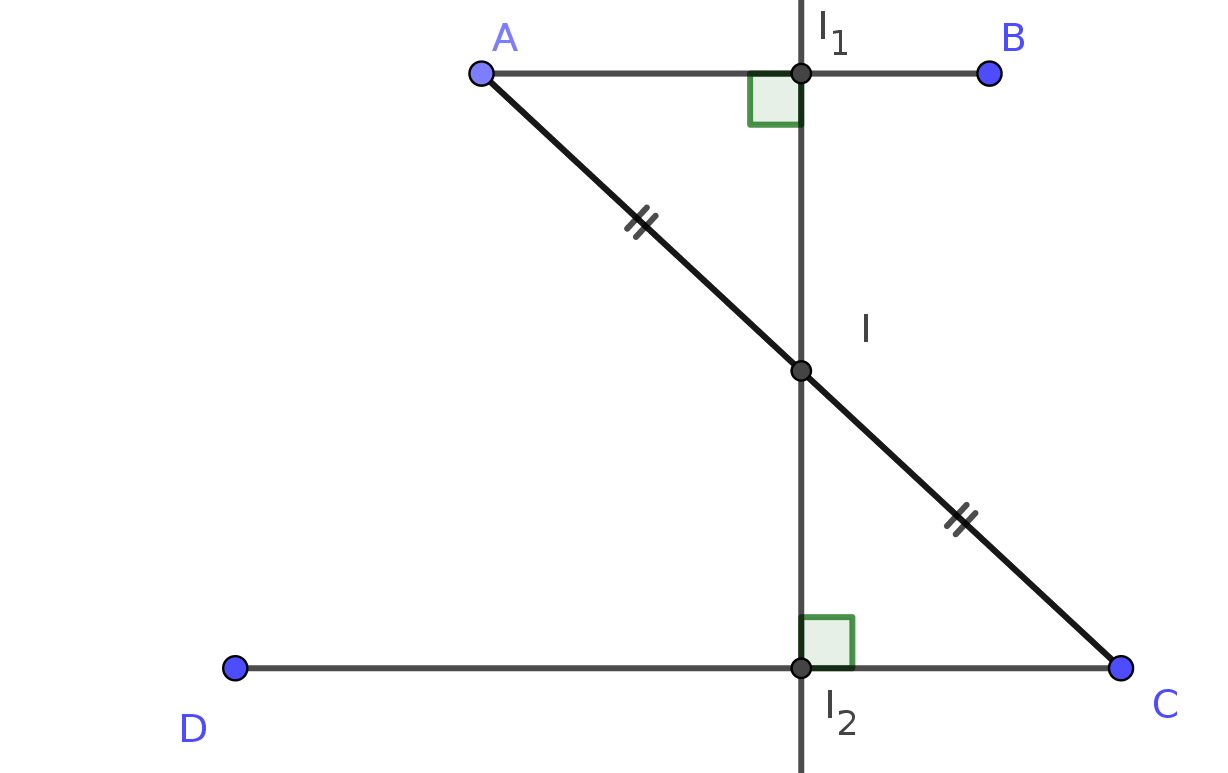
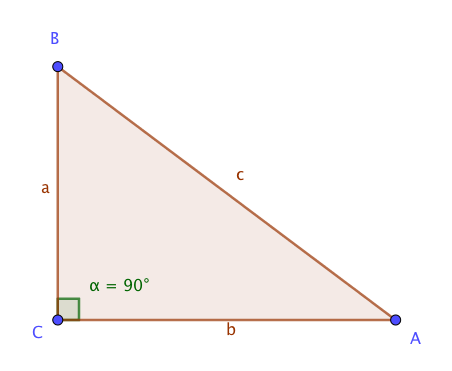
On montre en utilisant le théorème de Thalès(figure 2) que $\frac{II_1}{II_2}=\frac{IA}{IC}= 1$
(on rappelle que I est le milieu de $[AC]$) le point $I$ est donc le milieu de $I_1I_2$ et est à égale distance des droites $(AB)$ et $(CD)$
On montre de même que $J$ est à égale distance des droites $(AB)$ et $(CD)$.
On en déduit alors que la droite $(IJ)$ est parallèle à $(DC)$ ( et donc à $(AB)$
On applique maintenant le théorème de Thalès dans les triangles $KDC$ et $KIJ$ ($(IJ)//(DC)$)
On trouve $\frac{IJ}{DC} =\frac{KI}{KD}$ donc $\frac{KI}{KD}=\frac{1}{5}$
On en déduit que $KI$ est quatre fois plus grand que $ID$ et comme $ID=IB$
on en déduit aussi que $NB$ est trois fois plus grand que $NB$
Si on applique maintenant le théorème de Thalès dans les triangles $KIJ$ et $KAB$, on trouve $\frac{IJ}{AB} = \frac{KI}{KD}$
soit $\frac{3}{AB}= \frac{1}{3}$ et donc $AB= 9$

Auteur : Alexandre GROLLIER

Enoncé de l'énigme n° 5 (Lycée 1)

Si ABCD est un carré de côté 3 cm, quelle est l'aire de la région coloriée ?

Correction de l'énigme n° 3 (Lycée 2)

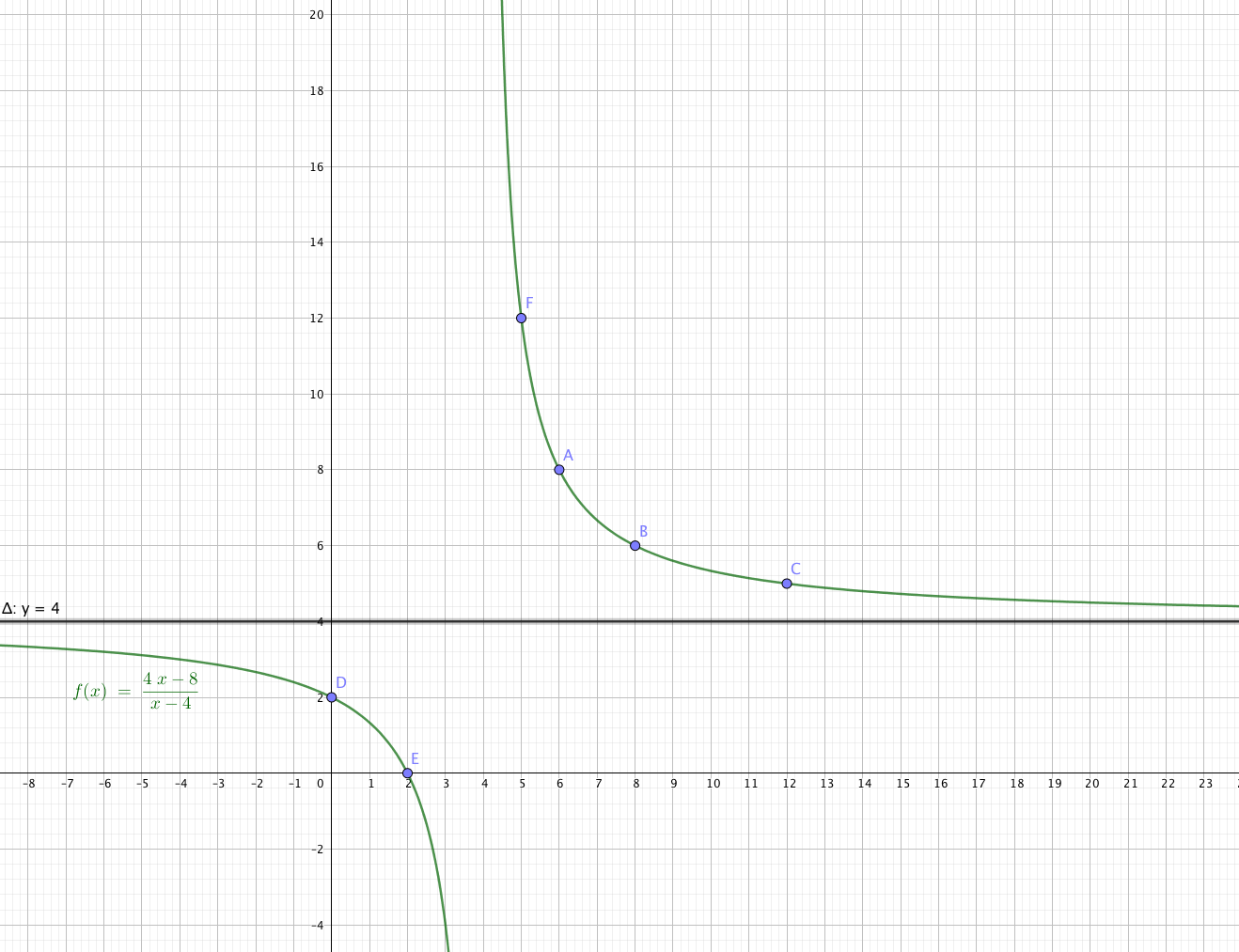
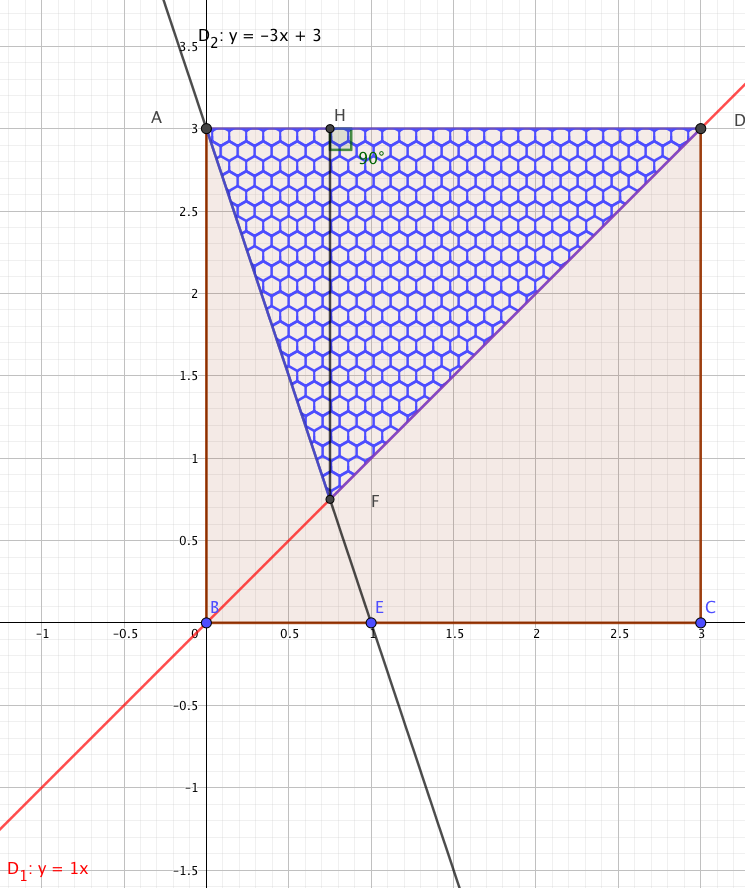Avec les notations de la figure ci-dessus, l'aire du triangle FAD vaut : $\mathcal{A}= \dfrac{AD\times FH}{2}= \dfrac{3}{2}FH$.
Calulons alors les cooronnées de $H$, point se trouvant à l'intersection des droites $(BD)$ et $(AE)$.

• Equation de $(BD)$:
  cette droite passe par l'origine O et a pour coeffifficient directeur 1.
  Ainsi (BD): $y=x$
• Equation de $(AE)$:
  son coefficient directer est -3.
  et a pour équation réduite : $y-y_A= m(x-x_A)$, soit $y-3=-3(x-0)$
  Ainsi (AE): $y=-3x+3$
• Coordonnées de H: $$\left\lbrace \begin{array}{l} y=x\\ y=-3x+3 \end{array} \right.\iff \left\lbrace \begin{array}{l} y=x\\ x=-3x+3 \end{array} \right. \iff \left\lbrace \begin{array}{l} y=x\\ x=\frac{3}{4} \end{array} \right.\iff \left\lbrace \begin{array}{l} y=\frac{3}{4}\\ x=\frac{3}{4} \end{array} \right.$$ Ainsi $H\left( \dfrac{3}{4}; \dfrac{3}{4}\right) $.
• Alors $FH= 3- \dfrac{3}{4}= \dfrac{9}{4}$, puis l'aire coloriée vaut $\mathcal{A}= \dfrac{3}{2}\times \dfrac{9}{4}= \dfrac{27}{8} $.

Auteur : Luc Giraud

Enoncé de l'énigme n° 3 (Lycée 2)

Déterminer combien il y a de triangles rectangles dont les côtés ont des longueurs entières et telles que leur aire soit égale à leur périmètre.

Correction de l'énigme n° 3 (Lycée 2)

On utilise la figure d'étude ci-dessous: Si $a, b$ et $c$ sont solutions du problème alors en notant $c$, le plus grand côté on a : $$\left\lbrace \begin{array}{l} c^2=a^2+b^2\\ \dfrac{1}{2}ab= a+b+c \end{array} \right. \iff \left\lbrace \begin{array}{l} c^2=a^2+b^2 \quad (1)\\ c =\dfrac{1}{2}ab -a-b\\ \end{array} \right. $$ $$\begin{array}{rl} (1)&\iff \left( \dfrac{1}{2}ab -a-b \right) ^2= a^2+b^2\\ & \iff \left( ab -2a-2b \right) ^2= 4a^2+4b^2\\ &\iff a^2b^2+4a^2+4b^2-4a^2b -4ab^2+8ab= 4a^2+4b^2\\ &\iff a^2b^2 -4a^2b -4ab^2+8ab=0\\ &\iff ab\left( ab-4a-4b+8\right) =0 \end{array}$$ On écarte le cas où un des côtés a une longueur nulle; ainsi $a\neq 0$ et $b\neq 0$, on déduit donc $$ ab-4a-4b+8 =0$$ $$\begin{array}{rl} (2)&\iff ab-4a-4b+8=0 \\ & \iff b(a-4)=4a-8 \\ &\iff b=\dfrac{4a-8}{a-4}\\ \end{array}$$ $a\neq4$, car $a=4$ donne $b\times 0= 4a-8$, soit $a= 2$, d'où une contradiction.
Donc si $(a,b)$ est un couple solution alors $b=\dfrac{4a-8}{a-4}$, ce qui signifie que le point $M(a,b)$ est sur l'hyperbole d'équation $y= \dfrac{4x-8}{x-4}.$
Etudions les variations de la fonction $f: x\mapsto \dfrac{4x-8}{x-4}.$ $f$ est dérivable comme quotient de deux fonctions dérivables dont le dénominateur ne s'annule pas. $f=\dfrac{u}{v}$ d'où $f'=\dfrac{u'v-v'u}{v^2}$ avec pour tout réel $x$, dans $ \mathbb{R} \backslash \{4\}$ : $\left\{ \begin{array}{l} u(x)~ = 4x-8\\ v(x)~ =x-4 \end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(x)~ =4 \\ v'(x)~ =1 \end{array}\right.$ $$ \begin{array}{cl} f'(x)&=\dfrac{4(x-4)-1(4x-8)}{(x-4)^2} \\ & =\dfrac{-8}{(x-4)^2} \\ \end{array} $$ Clairement $f'(x)<0$ sur chacun des intervalles où elle est définie.
Ainsi la fonction $f$ est strictement décroissante sur chacun des intervalles où elle est définie.
On déduit le tableau de variation de $f$:

Puis un tracé permet de lire les points à coordonnées entières sur l'hyperbole.
La fonction $f$ étant strictement décroissante sur $]4;+\infty[$, on déduit si $x>12$ alors $f(x)<f(12)$ soit $f(x)<5$.
On peut écrire $f(x)= 4+ \dfrac{8}{x-4}$, pour montrer que $f(x)<4$ sur $]12; +\infty[$.
On a donc montré que si $x\in ]12;+\infty[$,alors $4<f(x) <5$.
Ainsi l'hyperbole d'équation $y= \dfrac{4x-8}{x-4}$ ne possède pas de points à coordonnées entières dont l'abscisse appartient à $]12;+\infty[$.
Les seules solutions possibles sont donc à chercher dans l'intervalle $[1;12]$.
On obtient les triplets : $(5;12;13);(6;8;10);(8;6;10)$ et $(12;5;13)$.
On vérifie que chacun d'eux convient :

• $5^2+12^2=25+144=169=13^2$ et $\dfrac{1}{2}5\times 12 = 5+12+13$
• $6^2+8^2=36+64=100=10^2$ et $\dfrac{1}{2}6\times 8 = 6+8+10$

Auteur : Luc Giraud