Semaine des Maths 20017-2018 ; le lundi 12 mars, correction de l'énigme 1 ( Lycée 2)
Enoncé de l'énigme n° 1 (Lycée 2)
Les nombres indiquent les aires des zones coloriées exprimées en cm2. Combien vaut x ?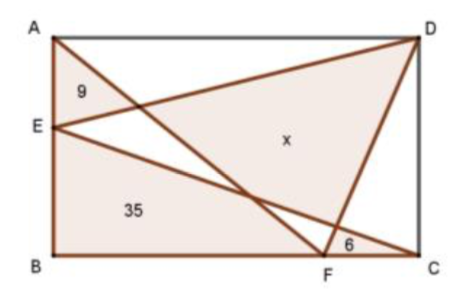
Correction de l'énigme n° 1 (Lycée 2)
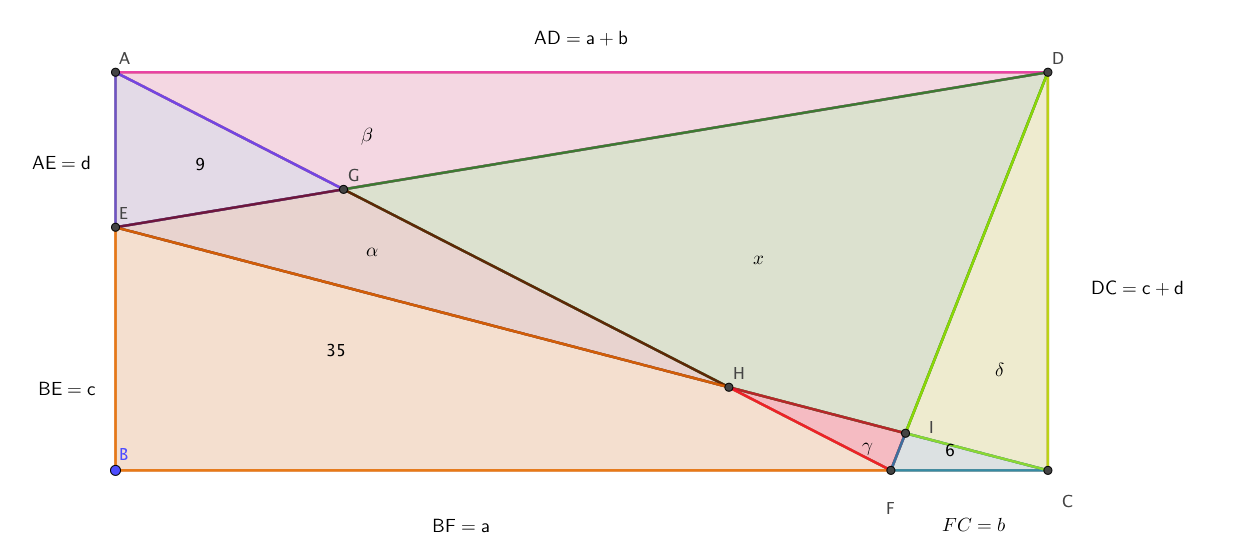
- On a dans le triangle (AED) en utilisant les notations de la figure : $$\dfrac{1}{2}(a+b)d=\beta+9\quad(1)$$
- Dans le quadrilatère (BFDE): $$ \dfrac{1}{2}(a+b)c =\gamma+35+6\quad(2)$$
- On note $\mathcal{A}$ l'aire du rectangle (ABCD): $$\mathcal{A}=\text{Aire}(ABCD)= (a+b)(c+d)$$
- $$(1)+(2) \text{ fournit } \dfrac{1}{2}(a+b)d+\dfrac{1}{2}(a+b)c= \beta +9+\gamma +41$$ $$ \dfrac{1}{2}(a+b)(c+d)=\beta +\gamma +50$$ $$ \dfrac{1}{2}\mathcal{A}=\beta +\gamma +50\quad (3)$$
- Dans le triangle (AFD), on peut écrire : $$x+\beta+\gamma=\dfrac{1}{2}(a+b)(c+d)$$ $$\text{ soit }x+\beta+\gamma=\dfrac{1}{2}\mathcal{A}\quad (4) $$
- De (3) et (4), on déduit $$\beta +\gamma +50= x+\beta+\gamma$$ $$\text{ soit }x=50$$
Auteur : Lionel DARIE